单纯形法是针对求解线性规划问题的一个算法，这个名称里的'单纯形'是代数拓扑里的一个概念，可以简单将'单纯形'理解为一个凸集，标准的线性规划问题可以表示为:
min（or max） f(x)=cx
s.t. Ax=b
x>=0,b>=0
以上形式称为线性规划标准型，使用单纯型法时，如果约束条件含有不等式时需新增变量（松弛变量、人工变量）转化为标准型，min. f(x)=cx指求函数最小值（也可以是求最大值），x是一个Rn维向量代表有n个变量，线性规划问题主要是面向实际问题，x变量可以代表距离、成本、价格、数量等，线性规划问题中要求x大于等于0，c同样是一个Rn维向量，这样cx实际上就是一个线性函数f(x);s.t.代表subject to代表服从于意思，这里是指变量x需要满足的约束条件，A是一个Rm*n维矩阵，代表有m个等式约束。下面是一个约束是不等式的情形:
min -4x1-x2
s.t. -x1+2x2<=4
2x1+3x2<=12
x1-x2<=3
x1,x2>=0
求解上面这个问题只要初中数学知识即可，具体可以使用代数法或几何的方法轻松得到，考虑到实际问题当中变量x是多维的，约束条件也会比示例多的多，这就需要一个一劳永逸的算法能通过计算机来获得正解，单纯形法就是这样的一个算法。单纯形法最早由 George Dantzig于1947年提出，单纯形法对于求解线性规划问题是具有跨时代意义的，其实不仅仅是针对线性规划，对于非线性规划问题在求解的过程中也大量依赖单纯形法，George Dantzig本人也被称为'线性规划之父'，他是好莱坞电影《心灵捕手》的原型。
一、凸集及其性质介绍
1.1 凸集概念
单纯形可以理解为一个凸集，介绍单纯形法之前有必要先来了解一下凸集概念及其性质，在很多机器学习算法中都会穿插凸集的概念，凸集上求最优解是凸优化的一个分支，凸集对于简化问题是有重要意义的。凸集可以用图形表示为一个没有洞的联通区域，如下图所示：
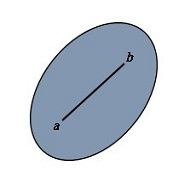
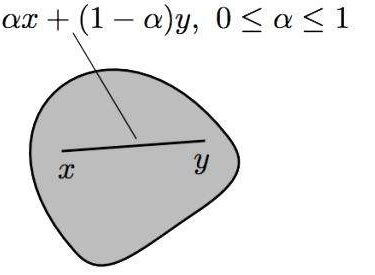
凸集也可以这样描述:用一条直线连接集合里两个元素，这条连线上的所有元素都在这个集合里，这个集合称为凸集；用代数公式表达是，对于任意x ,y
S,都有αx+(1-α)y
S（α>0）,则S为凸集:
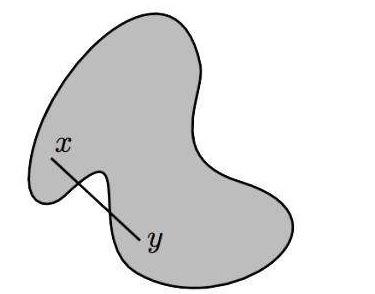
根据定义下面这个图形所定义的区域就不是凸集：
回过头来看线性规划的约束条件，将满足约束条件Ax=b的集合称为S,也称S为可行区域，对于其中任意x ,yS有:
Ax=b,Ay=b
x和y之间任意一个元素可以表示为 v= αx+(1-α)y,计算Av=A[αx+(1-α)y]=αb+b-αb=b,显然有v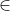
S，所以说线性规划中的约束条件描述的是一个凸集。
1.2 凸集的极点（顶点）
从凸集代数定义公式可以发现，凸集中任何一个点都可以用另外两个点线性组合而成，凸集中有一些特殊点用公式表达:x= αx1+(1-α)x2 x1 ,x2S,这时必有x=x1=x2,则称x为极点，或者形象的称为凸集的顶点；从图像上来看顶点不在凸集两个不同点连线上，如下图所示：
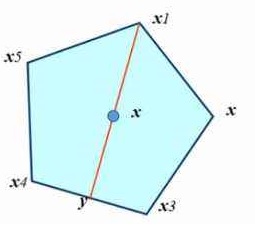
这里的x1,x2,x3,x4,x5都是顶点,而x不是顶点，特殊的，圆形上的圆周上每点都是顶点，所以说凸集上顶点可以是有限的，也可以是无限多的。在线性规划问题中，我们也把上面凸集称为可行区域，上图x1,x2,x3,x4,x5称为可行区域的顶点，x称为可行点。
对于凸集还有其他一些概念，虽然在单纯形法中没有用到，这里可以顺带提一下，凸集的区域范围可以有界或者是无界的，当凸集有界时，线性规划目标函数是把两个Rn维向量做内积运算得到一个实数R,所以这里本质上是一个有界线性泛函过程，如果没有约束条件的话，显然x向量与c向量呈180度相反方向时可得到最小值，c在这里可以理解为目标函数的梯度。
当凸集无界时这时需要引入方向的概念,设x是Rn维向量，x沿着一个方向延伸得到新的一个点v：v=x+αd x
S;α>0;d>0，如果新的点vS,则称d为可行方向。从线性代数角度来看，方向作为一个向量，可以由其他的方向线性合成，如果凸集一个方向不能由其他方向合成则称这个方向为极方向，这句话也可以反过来理解，凸集的所有可行方向都可以由极方向线性表示，极方向与极点有着对应关系。凸集的可行方向对于理解'可行区域求最优解'、'KKT条件'等非线性规划有着重要的意义。
二、单纯形法原理
2.1 可行解、最优解、基本可行解
根据上面的描述凸集中每个元素都满足约束条件，凸集中每个元素称为目标函数的可行解，显然可行解的数量是非常多的，可行解带入目标函数后一般得不到函数的最小值或最大值；如果可行解带入目标函数后可得到最值（最大或最小值），那么这个可行解就成为最优解。接下来介绍基本可行解，基本可行解是实现单纯形法的关键，还是以上面的问题为例，我们新增三变量x3,x4,x5使得约束条件变为等式标准型：
min -4x1-x2+0x3+0x4+0x5
s.t. -x1+2x2+x3+0x4+0x5=4
2x1+3x2 +0x3+x4+0x5=12
x1-x2 +0x3+0x4+x5=3
x1,x2,x3,x4,x5>=0
这里引入的x3,x4,x5称为松弛变量，松弛变量同样是大于等于0的变量，这时原问题常数向量c=[-4,-1,0,0,0],由于引入松弛变量系数都是0，所以新的目标函数和原目标函数是完全等价的，这时约束条件系数是矩阵A=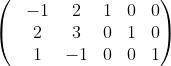
秩为3，A表示的是一个三维空间，如果将后面三列单位矩阵作为这个三维空间的三个基（也可以理解为三维空间三个坐标轴），那么A前面2列所代表向量可以通过这个单位矩阵线性表示出来，当然也可以将矩阵A中任意三列作为三维空间的基，将A中列分成两类，一类列是线性空间的基用B表示，一类列不是基用N表示，这样约束条件可写成矩阵形式：
上面公式中将与基B相乘的变量x3,x4,x5称为基变量，基变量一般用xB表示；与基N相乘的变量x1,x2称为非基变量一般用xN表示，每一个变量都与B或N中一个列对应，上面的公式也可以写为:
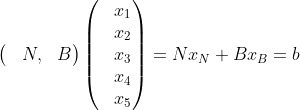
如果令xN=0,则有
,本例中B是R3*3满秩矩阵，即B有逆矩阵B-1,可得
。约束条件中要求x>=0,如果此时恰好有B-1b>=0也就满足了所有约束条件，x=（xN,xB）=（0,0，xB）也是目标函数的一个可行解，由于此时非基变量都为0，我们称这个可行解为基本可行解,由此可见基本可行解中'基'字指此时可行解基变量不全为0，而非基变量皆为0，请注意（0,0，xB）是基本可行解，xB是基本可行解中非0的分量集合，xB本身并不是基本可行解。
从线性空间的角度来理解线性规划问题，目标函数在新增松弛变量后x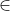
R5，即目标函数中的x是一个来自5维空间的向量，Ax=b的含义是通过线性映射将一个5维空间的向量映射为一个固定的三维向量 b,当然从函数角度来看这个映射过程是多对一的关系，即有许多个5维的向量线性映射后变为一个三维向量b,这些5维向量组成的集合之前已经介绍过，是一个凸集，而目标函数的含义此时可以表述为，在这个5维空间组成的凸集中找到一个或多个向量，与一个固定向量c的内积最小。
2.2 基本可行解、凸集顶点（极点）
基本可行解与凸集顶点是等价的，而凸集的顶点在线性规划问题中与最优解又有着密切的联系，首先来证明一个定理：凸集中元素x是基本可行解的充分必要条件为x是凸集的顶点。这个定理是实现单纯型法的关键，下面来详细证明一下：
先来证明这个定理必要性:即基本可行解一定是凸集的顶点，设x是基本可行解，根据之前分析可以知道向量x中必有前k个分量大于0，其余分量等于0，这个k个分量对应的是矩阵k个线性无关的列（基），设可行区S内有x1,x2,x1≠x2,根据凸集的定义设基本可行解x=αx1+(1-α)x2,由于基本可行解x前k个分量大于0而其余的分量等于0，又由于α选择的任意性，所以当i>=k+1时，必有x1[i]=x2[i]=0 (x1[i]代表x1第i个分量)。又因为Ax1=Ax2=b，即A(x1-x2)=0,已经知道x1,x2的分量从k+1开始都是0，此时就可以得到
，这里Ai是矩阵中几个线性不相关的列，前面已经知道x1≠x2，则Ai的系数x1[i]-x2[i]必然有不等于0的情形，而如果出现不等于0情况说明这些列Ai是线性相关的，这显然与假设矛盾，所以此时可以得到一个结论，没有两个不同的点x1,x2使得x=αx1+(1-α)x2等式成立，要使等式成立必须x=x1=x2,满足这个条件时x显然是凸集顶点（极点）。
接下来证明充分性：x是凸集的顶点则x一定是基本可行解。设x有k个分量大于0，其余等于0，由于约束条件要求x分量必须大于等于0，这样分类显然是成立的。 如果这个k个分量对应矩阵的列是线性无关的，那么顶点x就是基本可行解，这里我们可以用反证法，先假设k个分量对应矩阵列是线性相关的，即存在一个分量不全为0的向量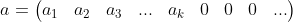
使得有等式：
，对于顶点x而言，前k分量也有相应的等式: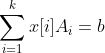
,联合这两个等式同时引入一个实数b，b>0,得到下面两组等式：
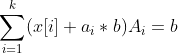
这样就从顶点x构造出2个新的向量x1,x2,观察上面的等式可以得到x1=x-ab,x2=x+ab，这里顶点x是向量，由于向量a是不全为0的向量且b是正实数，必然有x1≠x2；通过x1,x2可以反过来得到x的表达式x=x1/2+x2/2,因为x1≠x2这样等式显然与x是顶点的定义矛盾，此时就推翻最初假设得到新的结论：k个分量对应矩阵列是线性不相关的，这也同时证明了凸集的顶点则x一定是基本可行解。
2.3 凸集顶点与最优解
线性规划的目标函数是一个线性函数f(x)=cx,这个函数如果没有约束条件的束缚，其值域是正负无穷的，线性函数在定义域上等值线是相互之间平行的向量，等值线不会像非线性规划那样范围逐渐变小，进而变成一个点，这也导致了线性规划问题最值有可能是多个，加入约束条件后，目标函数最值只能在一个凸集中选择，线性规划的等值线运动过程如下图所示：
其中虚线代表目标函数f(x)=cx的等值线，ABCD所包含区域即为满足约束条件的凸集，箭头的方向代表目标函数的梯度，在线性规划问题中这个梯度就是向量c。当虚线沿着箭头方向平移时代表目标函数值不断变大，如果是求最小值则沿着箭头反方向移动，当然这个平移是有限制的，即不能离开凸集所在区域ABCD，最终目标函数一定在顶点A处取得最小值。
我们可以得到这样一个结论，线性规划问题的最值一定在凸集的顶点处。通过之前的分析已经知道，凸集的顶点是满足约束条件的基本可行解，单纯形法的核心思想可以归纳为：找到每一个基本可行解，代入目标函数后计算函数值取其最大或最小值即可。单纯形法上从代数角度是寻找约束条件的每一个基本可行解，从几何意义上来说是遍历凸集的每一个顶点，根据算法的特性有时也称为转轴法。
三、单纯形法的实现
3.1 入基、出基
单纯形法过程就是不断找出基本可行解的过程，基本可行解有一个显著的特征：基变量不为0，非基变量都为0。利用这个特性我们能够很快的找出每一个基本可行解。还是之前的标准型为例：
min -4x1-x2+0x3+0x4+0x5
s.t. -x1+2x2+x3+0x4+0x5=4
2x1+3x2 +0x3+x4+0x5=12
x1-x2 +0x3+0x4+x5=3
x1,x2,x3,x4,x5>=0
约束条件系数矩阵A是一个秩为3的矩阵，代表A是一个有3个基的3维线性空间，约束条件可以描述为A矩阵作用于一个5维向量x1,x2,x3,x4,x5后得到一个三维向量b=(4,12,3),这说明A矩阵是一个线性映射过程，将原来有5个基线性空间线性映射为一个3个基的线性空间，原来5维空间有2个基在线性映射后变成了0，这当然不是偶然的，因为线性映射有一个特性：零空间的维度（原来空间被映射为0的个数）+值域的维度（映射后空间的维度，本例是3）=A的列数（原来空间的维度），这个定理可以通过反证法来证明，这里不详细介绍。
基本可行解的特性决定了在原来5维空间中，每个顶点的形式一定是有3个分量大于0，另外2个等于0，所以顶点形式按排列组合则最多有
种，这与线性映射的机制完全吻合，我们不妨设原来5维空间有5个标准正交基：
假设一个在5维空间凸集中有一个顶点x形式为 (x1,x2,x3,0,0)，写成向量与坐标相乘的形式：
经过线性映射后原线性空间的3个5维基向量被映射为3个3维基向量，另外有2个基被映射为0向量：
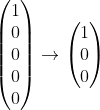
线性映射后新向量也可以写成基变量与单位矩阵相乘的形式：
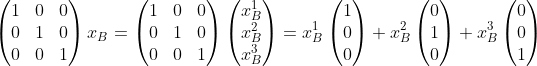
以上线性映射过程中产生了两个数学模型，一个是凸集空间，一个是线性方程模型，5维空间中顶点与线性方程中基本可行解一一对应，这个总结中一一对应非常重要，一一对应从函数角度来说是满射、单射，是可逆的，凸集顶点x:(x1,x2,x3,0,0)形式决定线性映射的方式，从而决定了xB；同样的也可以通过调整xB逆向得到5维空间中不同的顶点，xB是约束条件中基本可行解中大于0的分量，也就是说不断调整基本可行解就可以得到相应的5维空间中不同的顶点，这就像一系列联动的齿轮轴组，调节一端就可以影响另一端，这样一来就能很好理解单纯形法为什么也叫转轴法了。
说明基本可行解时说过，xB是在矩阵A中选择三个列作为单位矩阵得到的，同时提到，也可以选择矩阵其他的列作为3维空间的基，选择不同列作为3维空间基即可产生不同的xB，从而得到5维空间不同的顶点。新选择列称为入基，被替代的列称出基，这种替换的可以有许多种方式，使用暴力方法逐个迭代每一个顶点也可以实现，而当求解最小值问题时，如果借助梯度的概念，在得到一个顶点后，切换下一个顶点方向是函数变小的方向无疑会节省很多时间。
约束条件系数矩阵A中将作为基的列集合记作B，不是基的列集合记作N,则有A=(N，B),同样把x分量中基变量的集合记作xB，非基变量集合记作xN,约束条件可以写成： (N，B)（xN，xB）=b,这样可以得到等式 NxN+BxB=b,矩阵B是基矩阵且可逆，得到:
xB=B-1b - B-1NxN ⑴
当xN=0 时显然有xB=B-1b ，如果此时有B-1b>0则称xB是初始基本可行解,目标函数中同样将向量c也分成两部分，基变量对应系数记为cB, 非基变量对应的系数记为cN,这样就得到目标函数另一种形式：
f(x)=cBxB+cNxN ⑵
带入公式（1）后得到目标函数另一种形式:
如果此时有初始基本可行解，可得到f(x)=cBxB=cBB-1b。对上面的函数求导得：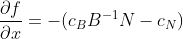
，
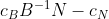大于0时导数小于0，说明在取初始基本解后目标函数还有变小的空间，这时可以选择矩阵非基集合中一列来代替现有基，即选择入基，如何选择入基呢?函数的微分形式有：
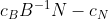越大则导数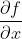
越小,目标函数变小的幅度就越大，将此作为选择入基的标准，遍历每个非基列pj,由于每次都只一个列作为入基，xN其他分量依然为0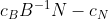，简化为cBB-1pj-cj,引入每一个待选列的检验量tj=cBB-1pj-cj, 如果检验量大于0，就选择这其中检验量最大的列作为入基就能保证目标函数变小，如果待选列的检验量都小于等于0则代表此时已经得到最小值。
入基已经准备就绪如何选择出基呢，即如何选择被替代的基列？在选择入基时其实还有一个隐含的问题，入基被选择后，新的基变量值是多少？这些可以从公式（1）中得到答案。
根据以上分析过程完成开篇线性规划问题，制成python代码如下：
import numpy as np
BASEINDEX=2
#列变换实现单纯形法
def simplex_ColTranslate(c ,A,b,flagstable):
B=A[:,BASEINDEX:]
Binv=np.linalg.inv(B)
xb=np.dot(Binv ,b)
cb=c[:,BASEINDEX:]
f=np.dot(cb,xb )
Inbaseindex=-1
OutBaseIndex = -1
tempvalue=0
for i in range(BASEINDEX):
v=np.squeeze(np.dot(np.dot(cb,Binv),A[:,i])-c[:,i],0)
if tempvalue<=v:
#找出入基
tempvalue=v
Inbaseindex=i
if tempvalue==0:
#找到最优解
return xb,f,c,flagstable
else:
#入基出基替换，同时交换系数c
y=np.dot(Binv,A[:,Inbaseindex])
minivalue=None
for i in range(y.shape[0]):
if y[i]>0:
x=xb[i]/y[ i]
#找出最小值，保证xb>=0
if minivalue is None or minivalue>x :
minivalue=x
OutBaseIndex=i+BASEINDEX
for i in range(A.shape[1]):
if i==OutBaseIndex:
for j in range(A.shape[0]):
tmp=A[j,i].copy()
A[j,i]=A[j, Inbaseindex]
A[j, Inbaseindex]=tmp
tempc= np.squeeze( c[:,OutBaseIndex],0).copy()
c[:,OutBaseIndex]=c[:,Inbaseindex]
c[:,Inbaseindex]=tempc
flagstable[OutBaseIndex-BASEINDEX]=Inbaseindex
return simplex_ColTranslate(c, A, b,flagstable)
def useColTranslate():
BASEINDEX = 2
c = np.array([[-4, -1, 0, 0, 0]],dtype=np.float)
A = np.array([[-1, 2, 1, 0, 0], [2, 3, 0, 1, 0], [1, -1, 0, 0, 1]],dtype=np.float)
b = np.array([[4], [12], [3]],dtype=np.float)
# 记录下标变动情况
flagstable = {}
for i in range(c.shape[1] - BASEINDEX):
flagstable[i] = BASEINDEX + i
x, f, c, flags = simplex_ColTranslate(c, A, b, flagstable)
print('最优解:%.2f' % (f[0, 0]))
for j in range(x.shape[0]):
print('x%d=%.1f' % (flags[j] + 1, x[j, 0]))
if __name__ == '__main__':
useColTranslate()运行结果如下：
3.2 单纯形法的表格方法
上面代码中设置了一个常量BASEINDEX用以指示A矩阵中基矩阵的开始索引，此后通过检验量将入基替换出基，将新的列置换出去，同时更新目标函数中的c向量的顺序，将cB与cN中分量同时完成置换，c中分量与x中分量如影随行，上面算法本质上是通过矩阵列变换实现单纯形法，好处是容易理解，与数学推导过程完全一致，弊端是打乱了原来矩阵列的顺序，不易于二次利用其中的参数，如在接下来介绍的两阶段法中需要二次利用矩阵A，列变换的处理方式为后期处理带来较大很大的难度。
余下文章请去往链接