这是在学习吴恩达的机器学习课程时,一些随笔。
课程地址在 coursera ML
文章目录
- 监督学习 VS 无监督学习
- Cost function
- 梯度下降
-
- 多元梯度下降
-
- 特征和线性拟合
- Normal Equation 正规方程
- 梯度下降 VS Normal Equation
- 数学建模中的回归问题
- 编程练习 ex1
监督学习 VS 无监督学习
简单来说:
- 监督学习:我们有一组数据集,并且已经知道了正确的 output,以及 input 和 output 之间的关系。我们期望根据已有的数据确定一个 input 到 output 的映射关系 (
x
⟶
f
(
x
)
x \longrightarrow f(x)
x⟶f(x)) ,从而对一组新的 input 求出 output。
监督学习通常分为“回归”和“分类”问题。 - 无监督学习:有时候我们只有一组数据,而不知道这一组数据任何对应的 output。这时候我们期望通过无监督学习从数据中获取一些特征,并根据这些特征对数据分类。无监督学习通常为“聚类”问题。
Cost function
在回归模型中,可以通过代价函数来衡量拟合的优度。
对一组数据集,如果选取函数
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_\theta(x)=\theta_0+\theta_1x
hθ(x)=θ0+θ1x 来拟合,那么对于选取的每一组
θ
1
,
θ
2
\theta_1, \theta_2
θ1,θ2 ,其对应的代价函数形如:
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
y
^
i
−
y
i
)
2
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
2
J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}_{i}-y_{i}\right)^{2}=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)^{2}
J(θ0,θ1)=2m1i=1∑m(y^i−yi)2=2m1i=1∑m(hθ(xi)−yi)2
即每一个 input
x
i
x_i
xi 的拟合值
h
0
(
x
i
)
h_0(x_i)
h0(xi) 和 实际值 output
y
i
y_i
yi 差的平方和再除以样本点的两倍
2
m
2m
2m。(可以抽象为平均距离,样本点和拟合点的距离越小,则拟合得越好)
我们的目的是选取一组适当的
θ
1
,
θ
2
\theta_1, \theta_2
θ1,θ2 以使成本函数值最小,即达到最优拟合优度。
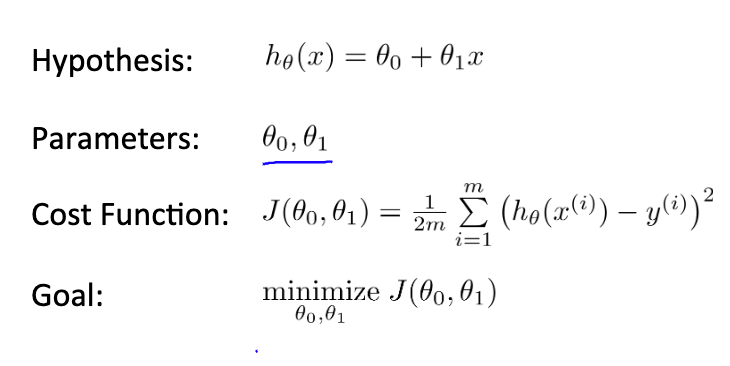
梯度下降
该怎样求得这样一组“适当的
θ
1
,
θ
2
\theta_1, \theta_2
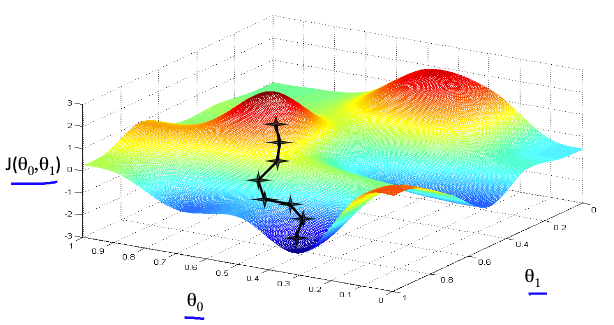
θ1,θ2 ” 呢?梯度下降算法给出了一个不错的解决方案。
梯度下降为了求解出成本函数
J
(
θ
0
,
θ
1
)
J\left(\theta_{0}, \theta_{1}\right)
J(θ0,θ1) 关于
θ
1
,
θ
2
\theta_1, \theta_2
θ1,θ2 的最小值,是这样的做的:
- 先从随机选取的一个初始点 (
θ
1
,
θ
2
\theta_1, \theta_2
θ1,θ2) 开始;
- 在当前位置环顾四周,找到一个坡度最陡的下坡方向;
- 往这个下坡方向下降一定距离,到达一个新的位置;
- 重复第二步迭代,直到收敛(到达谷底)。
每次下降的最陡方向即为成本函数的导数,下降的步伐由学习率
α
\alpha
α 决定。梯度下降以该式更新
θ
\theta
θ ,直到收敛:(方向导数即是函数值沿该方向变化的最大速度,参见 微积分-梯度)
θ
j
:
=
θ
j
−
α
∂
∂
θ
j
J
(
θ
0
,
θ
1
)
\theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J\left(\theta_{0}, \theta_{1}\right)
θj:=θj−α∂θj∂J(θ0,θ1)
这个“下降”是
θ
1
\theta_1
θ1 和
θ
2
\theta_2
θ2 两个方向下降的矢量和(类比“力的合成”),并且每次迭代都应该同时更新
j
=
0
,
1
j=0,1
j=0,1 的
θ
\theta
θ 值。
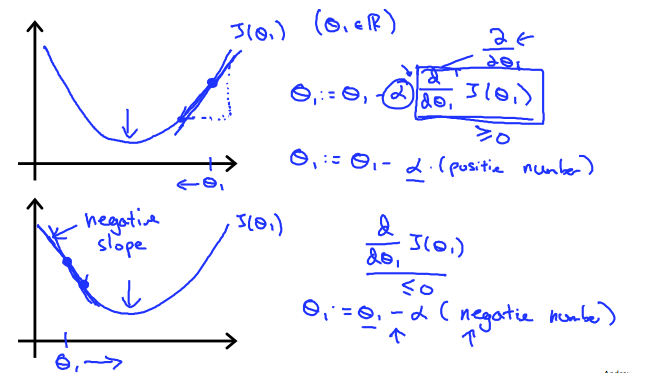
梯度下降算法总能正确地工作,以
θ
1
\theta_1
θ1 方向的分量来说明这件事:(注意学习率
α
\alpha
α 的值应该总取正值)
- 若
∂
∂
θ
1
J
(
θ
0
,
θ
1
)
\frac{\partial}{\partial \theta_{1}} J\left(\theta_{0}, \theta_{1}\right)
∂θ1∂J(θ0,θ1) 为正,则
θ
\theta
θ 将减去一个正数从而更加靠近斜率为 0 的点(收敛点);图中上部分
- 若
∂
∂
θ
1
J
(
θ
0
,
θ
1
)
\frac{\partial}{\partial \theta_{1}} J\left(\theta_{0}, \theta_{1}\right)
∂θ1∂J(θ0,θ1) 为负,则
θ
\theta
θ 将减去一个负数从而更加靠近斜率为 0 的点;图中下部分
- 而且非常巧妙的在于,随着越来越靠近收敛点,该方向的曲线斜率越来越小,这也就意味着该方向的方向导数
∂
∂
θ
1
J
(
θ
0
,
θ
1
)
\frac{\partial}{\partial \theta_{1}} J\left(\theta_{0}, \theta_{1}\right)
∂θ1∂J(θ0,θ1) 越来也小,从而使下降的步伐越来越小,避免跨过收敛点导致无法收敛(前提是选取了适当的学习率
α
\alpha
α )
梯度下降的完整算法形如:

当梯度下降用于线性回归时,求偏导后可得出新的形式:

你可能注意到了,梯度下降只能找到局部最小值。因此如果问题只有一个全局最优解,那么总能找到这个解;而若有多个局部最优解时,则可能需要选取多个不同的起始点多次梯度下降。
学习率
α
\alpha
α
为了使梯度下降良好地工作,我们需要选取一个合适的学习率
α
\alpha
α 。它不应该太大(这可能导致
J
(
θ
)
J(\theta)
J(θ)并不在每一次迭代后减少,甚至可能导致无法收敛),也不应该太小(这将导致收敛的很慢)。
为了检验我们选取的
α
\alpha
α 值是否合适,可以观察
θ
\theta
θ 值对应的最小成本函数
m
i
n
J
(
θ
)
min J(\theta)
minJ(θ) 是否随着迭代的次数而变小:

多元梯度下降
当 input 数据有多个属性时,拟合函数形如:
h
θ
(
x
)
=
θ
T
x
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
3
+
⋯
+
θ
n
x
n
h_{\theta}(x)=\theta^{T}x=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\theta_{3} x_{3}+\cdots+\theta_{n} x_{n}
hθ(x)=θTx=θ0+θ1x1+θ2x2+θ3x3+⋯+θnxn
成本函数和梯度下降和一元类似,使用向量表示更为贴切:

同样的将成本函数
J
(
θ
)
J(\theta)
J(θ) 分别对
θ
j
\theta_j
θj 求偏导(方向导数),即可得到线性回归特有形式的梯度下降通式:
θ
j
:
=
θ
j
−
α
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
⋅
x
j
(
i
)
for
j
:
=
0
…
n
\theta_{j}:=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{j}^{(i)} \qquad \text { for } \mathrm{j}:=0 \ldots \mathrm{n}
θj:=θj−αm1i=1∑m(hθ(x(i))−y(i))⋅xj(i) for j:=0…n
如你所见,对每一个
θ
j
\theta_j
θj 求偏导得到的是一个固定形式的表达式,它只跟
x
j
x_j
xj 有关。事实上在一元梯度下降中也是如此,只不过由于
x
0
x_0
x0 是一个常量 1 而省略了
x
0
x_0
x0 。下面是一元梯度下降和多元梯度下降的对比:

特征缩放和均值归一化
在进行多元梯度下降时,若不同属性之间的数量级相差非常大,将导致迭代次数非常多,收敛的非常慢。为了避免这样的问题,在进行多元梯度下降时非常有必要进行特征缩放。
缩放的方法有很多种,只要最终所有的数据都控制在一个较小范围内即可,这个范围通常没有绝对的要求,只要不是太小或者太大均可。
- 特征缩放:用输入值除以输入变量的范围(即最大值减去最小值),结果的范围是
−
1
∼
1
-1\sim1
−1∼1 ;
- 均值归一化:将输入值减去平均值后再除以输入变量的范围,结果是的范围近似是
−
0.5
∼
0.5
-0.5 \sim 0.5
−0.5∼0.5
特征和线性拟合
Normal Equation 正规方程
还记得我们的成本函数吗?
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
y
^
i
−
y
i
)
2
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
2
J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(\hat{y}_{i}-y_{i}\right)^{2}=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)^{2}
J(θ0,θ1)=2m1i=1∑m(y^i−yi)2=2m1i=1∑m(hθ(xi)−yi)2
我们拟合的目的就是选取一组合适的
θ
1
,
θ
2
\theta_1,\theta_2
θ1,θ2 使得
J
(
θ
1
,
θ
2
)
J(\theta_1,\theta_2)
J(θ1,θ2) 函数值最小。梯度下降给出了一套直观的解法,即不断(有规律)地尝试不同的
θ
1
,
θ
2
\theta_1,\theta_2
θ1,θ2 ,直到找到最合适的那一组。
等等,函数值最小?那不就是导数值为 0 吗?因此,正规方程解法将 “求成本函数值最小对应的
θ
\theta
θ ” 转换为求 “成本函数导数值为 0 对应的
θ
\theta
θ ” ,如果是多元函数,则是对每一个
θ
j
\theta_j
θj 的偏导数值为 0:

如果拟合函数为
h
θ
(
x
)
=
θ
T
x
=
θ
0
x
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
3
+
⋯
+
θ
n
x
m
h_{\theta}(x)=\theta^{T}x=\theta_{0}x_0+\theta_{1} x_{1}+\theta_{2} x_{2}+\theta_{3} x_{3}+\cdots+\theta_{n} x_{m}
hθ(x)=θTx=θ0x0+θ1x1+θ2x2+θ3x3+⋯+θnxm ,将 input 数据集对应到
X
X
X ,output 数据集对应到
y
y
y,则总可以这样求得最优的
θ
\theta
θ :
θ
=
(
X
T
X
)
−
1
X
T
y
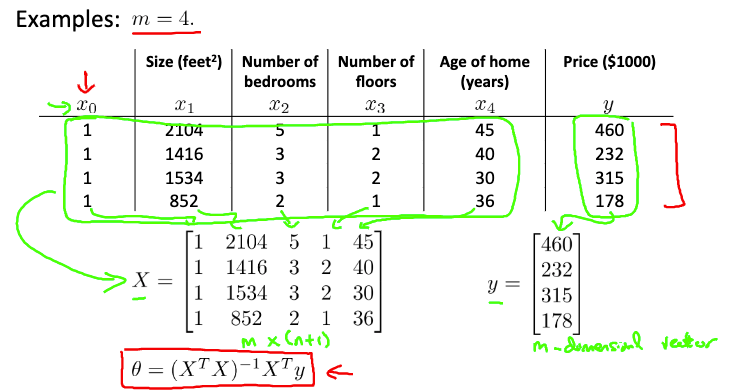
\theta=\left(X^{T} X\right)^{-1} X^{T} y
θ=(XTX)−1XTy
这是一个
m
=
4
m=4
m=4 时的例子(注意 input 数据集和 output 数据集到
X
,
y
X,y
X,y 的对应,这个例子中
θ
0
x
0
\theta_0x_0
θ0x0 是一个常数项,因此
x
0
x_0
x0 的输入是一个恒定值 1):
具体到利用 MATLAB 计算只有简单的一条命令:
% X' - 转置
% pinv(X) - 对 X 求伪逆
% 总可以通过该式求得正确的 theta,即使矩阵 X 不可逆
theta = pinv(X'*X)*(X')*y
% X\Y - 对 X 求逆后与 Y 相乘,因此也可以这样做:
theta = (X'*X)\(X')*y
使用正规方程解法求
θ
\theta
θ 将不用考虑 input 数据集之间的数量级,直接计算就好,不再需要特征缩放。
梯度下降 VS Normal Equation

看上去正规方程解法似乎比梯度下降简单的多也实用的多,只有当 input 数据集的属性 n 非常大时可能才需要考虑使用梯度下降。事实也是这样的,在一般的回归问题中,特征方程已经够用了。但这并不意味着学习的梯度下降是徒劳,在后面即将看到的很多其他问题还将不得不用到梯度下降。
数学建模中的回归问题
在回归问题中通常并不使用梯度下降法求解
θ
\theta
θ ,而使用正规方程解法。但可能有些术语上的出入:
- 一般把 Cost Function 称之为”均方误差“,对应了最常见的欧几里得距离或简称”欧氏距离“;
- 基于均方误差最小化来求解待定系数
θ
\theta
θ 的方法称之为”最小二乘法“;
- 最小二乘法的求解过程称为回归模型的最小二乘“参数估计”(求解过程与正规方程解法一致);
在回归问题中,最小二乘法就是试图找到一条曲线(或直线),使所有样本点到曲线上的欧氏距离之和最小。
完整的最小二乘法拟合参见司守奎的*《数学建模算法与应用》第二版* 92 页:


关于 MATLB 拟合函数、工具箱的使用参见另一篇笔记 MATLAB数学建模 回归与内插
编程练习 ex1
computeCost.m
function J = computeCost(X, y, theta)
%COMPUTECOST Compute cost for linear regression
% J = COMPUTECOST(X, y, theta) computes the cost of using theta as the
% parameter for linear regression to fit the data points in X and y
% Initialize some useful values
m = length(y); % number of training examples
% You need to return the following variables correctly
J = 0;
% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta
% You should set J to the cost.
y_fit = X * theta;
J = sum((y-y_fit).^2) / (2*length(y));
% =========================================================================
end
gradientDescent.m
function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)
%GRADIENTDESCENT Performs gradient descent to learn theta
% theta = GRADIENTDESCENT(X, y, theta, alpha, num_iters) updates theta by
% taking num_iters gradient steps with learning rate alpha
% Initialize some useful values
m = length(y); % number of training examples
J_history = zeros(num_iters, 1);
temp = zeros(size(theta));
mmin = computeCost(X, y, theta);
for iter = 1:num_iters
% ====================== YOUR CODE HERE ======================
% Instructions: Perform a single gradient step on the parameter vector
% theta.
%
% Hint: While debugging, it can be useful to print out the values
% of the cost function (computeCost) and gradient here.
%
thetatemp=theta; % 要同时更新所有 theta,因此用一个中间值记录下
for j=1:length(theta)
theta(j) = theta(j) - alpha / m * sum( (X*thetatemp-y) .* X(:,j) );
end
% ============================================================
% Save the cost J in every iteration
J_history(iter) = computeCost(X, y, theta);
if(J_history(iter)<mmin) % 如果当前 cost function 值更小,则更新 theta
mmin=J_history(iter);
temp=theta;
end
end
theta=temp;
end
本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容,请联系:hwhale#tublm.com(使用前将#替换为@)