最近在读了Joan Sola所写的Course on SLAM中有关因子图部分的介绍后，发现其中有关于因子图构建的思路觉得很有意思，因此在这里记录一下。
首先简单地介绍一下如何将一个SLAM问题建立成为一个DBN（Dynamic Bayes Network 动态贝叶斯网络）。DBN是一种统计模型，它可以用一个有向无环图来表示随机变量以及它们之间的依赖关系。它们之间的条件依赖可以用用箭头表示。比如
B
⟶
A
B\longrightarrow A
B⟶A代表A在B条件下的概率，无环则表示不会出现诸如A依赖于B，B依赖于C，C又依赖于A的情况。在SLAM问题中，我们有四种类型的随机变量：
其中运动模型表示为：
x
i
=
f
i
(
x
i
−
1
,
u
i
)
+
w
i
x_i=f_i(x_{i-1},u_i)+w_i
xi=fi(xi−1,ui)+wi用子图表示
x
i
x_i
xi在给定
x
i
−
1
x_{i-1}
xi−1以及
u
i
u_i
ui时的条件概率即为：
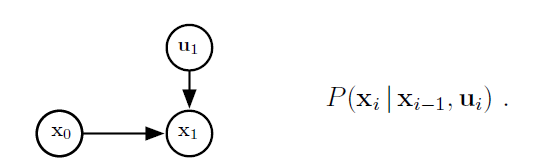
同样，测量模型可以表示为：
z
k
=
h
k
(
x
i
,
m
)
+
v
k
z_k=h_k(x_i,m)+v_k
zk=hk(xi,m)+vk用子图表示为：
m表示传感器对周围环境的测量值，在SLAM问题中经常表示为路标点的位置(landmark)，因此在传感器姿态为
x
i
x_i
xi时测量得到的路标点
l
j
l_j
lj的测量模型为：
z
k
=
h
k
(
x
i
,
l
j
)
+
v
k
z_k=h_k(x_i,l_j)+v_k
zk=hk(xi,lj)+vk此时子图可以表示为：
将所有的子图聚合在一起可以得到完成的DBN网络：
此时所有随机变量的联合概率写为：
P
(
X
,
L
,
U
,
Z
)
∝
P
(
X
0
)
∏
i
=
1
M
P
(
x
i
∣
x
i
−
1
,
u
i
)
∏
k
=
1
K
P
(
z
k
∣
x
i
k
,
l
j
k
)
P(X,L,U,Z)\propto P(X_0)\prod_{i=1}^{M}P(x_i|x_{i-1},u_i)\prod_{k=1}^{K}P(z_k|x_{i_k},l_{j_k})
P(X,L,U,Z)∝P(X0)i=1∏MP(xi∣xi−1,ui)k=1∏KP(zk∣xik,ljk)其中
P
(
x
0
)
P(x_0)
P(x0)表示初始时的先验概率，我们最终要优化的目标函数和状态量是：
{
X
∗
,
L
∗
}
=
arg
max
X
,
L
P
(
X
0
)
∏
i
=
1
M
P
(
x
i
∣
x
i
−
1
,
u
i
)
∏
k
=
1
K
P
(
z
k
∣
x
i
k
,
l
j
k
)
\{X^*,L^*\}=\arg\max_{X,L} P(X_0)\prod_{i=1}^{M}P(x_i|x_{i-1},u_i)\prod_{k=1}^{K}P(z_k|x_{i_k},l_{j_k})
{X∗,L∗}=argX,LmaxP(X0)i=1∏MP(xi∣xi−1,ui)k=1∏KP(zk∣xik,ljk)
联合概率问题可以转化表示成 M + K M+K M+K个因子组成的图，每一个因子由测量值（可以是控制量 U U U也可以是观察量 Z Z Z）产生，并且连接在不同的节点（位姿或者路标点或者两者都有）两端。所以一个因子图通常由两个节点组成：变量节点（variable）该节点由我们需要求解的变量组成，比如位姿或者路标点的位置，以及因子（factor），表示两个节点之间的约束关系。
已知运动和测量模型为：
因此每一个因子的条件概率写为：
我们可以将上边的条件概率（i.e factor）表示为更加紧凑的形式，令：
e
k
(
x
i
k
−
1
,
x
i
k
)
=
f
i
k
(
x
i
k
−
1
,
u
i
k
)
−
x
i
k
(1)
e_k(x_{{i_k}-1},x_{i_k})=f_{i_k}(x_{{i_k}-1},u_{i_k})-x_{i_k}\tag{1}
ek(xik−1,xik)=fik(xik−1,uik)−xik(1)
e
k
(
x
i
k
,
l
j
k
)
=
h
k
(
x
i
k
,
l
j
k
)
−
z
k
(2)
e_k(x_{i_k},l_{j_k})=h_k(x_{i_k},l_{j_k})-z_k\tag{2}
ek(xik,ljk)=hk(xik,ljk)−zk(2)
此时所有的因子可以写成一个统一的形式：
ϕ
k
=
exp
(
−
1
2
e
k
⊤
Ω
k
e
k
)
\phi_k=\exp(-\frac{1}{2}e_k^\top\Omega_ke_k)
ϕk=exp(−21ek⊤Ωkek)
这表明，只要我们可以从第k个测量值与状态量
i
k
i_k
ik和
j
k
j_k
jk里边计算得到误差项
e
k
e_k
ek
e
k
(
x
i
k
,
x
j
k
,
z
k
)
e_k(x_{i_k},x_{j_k},z_k)
ek(xik,xjk,zk)
那么该测量值具体是控制变量
U
U
U还是传感器的测量值
L
L
L就不重要了，换句话说，控制变量
U
U
U和测量值
L
L
L都可以作为测量值
Z
Z
Z构建因子。 有
K
K
K个测量值就有
K
K
K个因子。（注：这里的
K
K
K和上边表示路标点数量的
K
K
K我猜测应该不是一个
K
K
K，这里的
K
K
K表示控制变量和路标点数量的总和，而上边的K仅表示路标点的数量）
现在我们的待估计量为：
x
=
[
x
1
,
.
.
.
,
x
N
]
⊤
\mathbf{x}=[\mathbf{x}_1,...,\mathbf{x}_N]^{\top}
x=[x1,...,xN]⊤
x
i
=
{
X
i
,
L
i
}
,
i
∈
1
,
2
,
.
.
.
,
N
\mathbf{x}_i=\{X_i,L_i\},i\in1,2,...,N
xi={Xi,Li},i∈1,2,...,N
测量值为：
z
=
[
z
1
,
.
.
.
,
z
K
]
⊤
\mathbf{z}=[\mathbf{z}_1,...,\mathbf{z}_K]^{\top}
z=[z1,...,zK]⊤
z
j
=
{
U
j
,
Z
j
}
,
j
∈
1
,
2
,
.
.
.
,
K
\mathbf{z}_j=\{U_j,Z_j\},j\in1,2,...,K
zj={Uj,Zj},j∈1,2,...,K
此时的联合概率为：
P
(
x
,
z
)
∝
∏
i
=
1
K
ϕ
k
∝
∏
i
=
1
K
exp
(
−
1
2
e
k
⊤
Ω
k
e
k
)
P(\mathbf{x},\mathbf{z})\propto\prod_{i=1}^{K}\phi_k\propto\prod_{i=1}^{K}\exp(-\frac{1}{2}\mathbf{e}_k^{\top}\mathbf{\Omega}_k\mathbf{e}_k)
P(x,z)∝i=1∏Kϕk∝i=1∏Kexp(−21ek⊤Ωkek)
对该联合概率取负对数可以将
exp
(
⋅
)
\exp(·)
exp(⋅)消掉，得到：
x
o
p
t
=
arg max
x
∑
k
=
1
K
e
k
(
x
i
,
x
j
)
⊤
Ω
k
e
k
(
x
i
,
x
j
)
\mathbf{x}_{opt}=\argmax_{\mathbf{x}}\sum_{k=1}^{K}\mathbf{e}_k(\mathbf{x}_i,\mathbf{x}_j)^\top\mathbf{\Omega}_k\mathbf{e}_k(\mathbf{x}_i,\mathbf{x}_j)
xopt=xargmaxk=1∑Kek(xi,xj)⊤Ωkek(xi,xj)
从上边的推导中，当给定我们一个运动向量
u
i
\mathbf{u}_i
ui，我们可以利用运动模型构建运动误差为：
e
=
f
(
x
i
−
1
,
u
i
)
−
x
i
\mathbf{e}=f(\mathbf{x}_{i-1},\mathbf{u}_{i})-\mathbf{x}_i
e=f(xi−1,ui)−xi但是这样构建误差是有一个前提假设的，那就是高斯噪声
w
i
\mathbf{w}_i
wi在函数
f
(
⋅
)
f(·)
f(⋅)之外。即：
x
i
=
f
x
(
x
i
−
1
,
u
i
)
+
w
i
,
w
i
∼
N
(
0
,
Ω
)
(3)
\mathbf{x}_i=f_x(\mathbf{x}_{i-1},\mathbf{u}_i)+\mathbf{w}_i,\mathbf{w}_i\sim\mathcal{N}(0,\mathbf{\Omega})\tag{3}
xi=fx(xi−1,ui)+wi,wi∼N(0,Ω)(3)
但是显示情况中，我们更常见的却是如下的运动模型：
x
i
=
f
x
(
x
i
−
1
,
u
i
−
w
i
)
,
w
i
∼
N
(
0
,
Ω
)
(4)
\mathbf{x}_i=f_x(\mathbf{x}_{i-1},\mathbf{u}_i-\mathbf{w}_i),\mathbf{w}_i\sim\mathcal{N}(0,\mathbf{\Omega})\tag{4}
xi=fx(xi−1,ui−wi),wi∼N(0,Ω)(4)在这种情况下，我们常常做的是通过
f
(
⋅
)
f(·)
f(⋅)关于
w
i
\mathbf{w}_i
wi的
J
a
c
o
b
i
a
n
Jacobian
Jacobian将原函数线性化，即：
x
i
≈
f
x
(
x
i
−
1
,
u
i
)
+
∂
f
∂
w
w
i
(5)
\mathbf{x}_i\approx f_x(\mathbf{x}_{i-1},\mathbf{u}_i)+ \frac{\partial f}{\partial \mathbf{w}} \mathbf{w}_i\tag{5}
xi≈fx(xi−1,ui)+∂w∂fwi(5)
但是这样做非常容易发生由于
J
a
c
o
b
i
a
n
Jacobian
Jacobian不满秩而导致的协方差矩阵
Ω
\mathbf{\Omega}
Ω为奇异矩阵的错误（无法求逆），为了解决这个问题，我们通常避免
J
a
c
o
b
i
a
n
Jacobian
Jacobian的计算，即可以将误差项表示为如下的形式：
u
i
=
f
−
1
(
x
i
,
x
i
−
1
)
+
w
i
\mathbf{u}_i=f^{-1}(\mathbf{x}_i,\mathbf{x}_{i-1})+\mathbf{w}_i
ui=f−1(xi,xi−1)+wi
e
=
f
−
1
(
x
i
,
x
i
−
1
)
−
u
i
\mathbf{e}=f^{-1}(\mathbf{x}_i,\mathbf{x}_{i-1})-\mathbf{u}_i
e=f−1(xi,xi−1)−ui
该形式和之前测量值的误差表达式形式一致：
e
=
h
(
x
i
,
l
j
)
−
z
\mathbf{e}=h(\mathbf{x}_{i},\mathbf{l}_{j})-\mathbf{z}
e=h(xi,lj)−z
但是在一些特殊的传感器上（比如IMU），
f
−
1
(
⋅
)
f^{-1}(·)
f−1(⋅)可能不那么容易求得，此时我们就需要将测量值通过一个函数变形为：
z
=
z
(
u
)
\mathbf{z}=z(\mathbf{u})
z=z(u)，此时由控制变量得到的测量值写为：
z
i
=
g
(
x
i
,
x
i
−
1
)
+
w
i
\mathbf{z}_i=g(\mathbf{x}_i,\mathbf{x}_{i-1})+\mathbf{w}_i
zi=g(xi,xi−1)+wi
误差项变为：
e
=
g
(
x
i
,
x
i
−
1
)
−
z
i
\mathbf{e}=g(\mathbf{x}_i,\mathbf{x}_{i-1})-\mathbf{z}_i
e=g(xi,xi−1)−zi
由于IMU的测量值有6个自由度，因此导致
f
(
⋅
)
f(·)
f(⋅)的非线性效应十分严重，逆函数不容易求出，一个解决方法就是利用观测的差值，即先将IMU的读数进行数次预积分，以降低
f
(
⋅
)
f(·)
f(⋅)的维度，这样
f
(
⋅
)
f(·)
f(⋅)的逆函数就比较容易求得了。
