目录
1、观测器提出的背景
1.1 龙伯格观测器的物理意义
2、状态空间下龙伯格观测器设计
2.1 状态观测器设计
3. 状态观测器实例
3.1 直接法
4、控制器与观测器对比
4.1 基于状态反馈的控制器设计
4.2 基于输出反馈的控制器设计
4.3. 基于观测器的控制器
1、观测器提出的背景
控制理论中的大多数概念是基于传感器来测量被控量的,事实上在讲授控制理论时,通常假定可采用近乎完美的反馈信号,然而这一假设通常是不成立的,我们所使用的传感器,有的信号没法测量,有的信号测量的会引入误差,因此我们需要应对这些情况。
观测器可以用来补充或者取代控制系统中的传感器,所谓观测器并不是一种具体的器件,而是指结合感知信号与控制系统其他信息产生观测信号的一种算法,可以理解成一段程序,在有些情况下,观测器也可以用来提高系统性能,减少采样延迟,当然观测器技术也不是万能的,它增加了系统的复杂性,并且需要计算资源,同实际传感器相比,它的鲁棒性可能要差,但是熟练运用观测器仍然会带来许多好处。
1.1 龙伯格观测器的物理意义
经常被使用的是龙伯格观测器
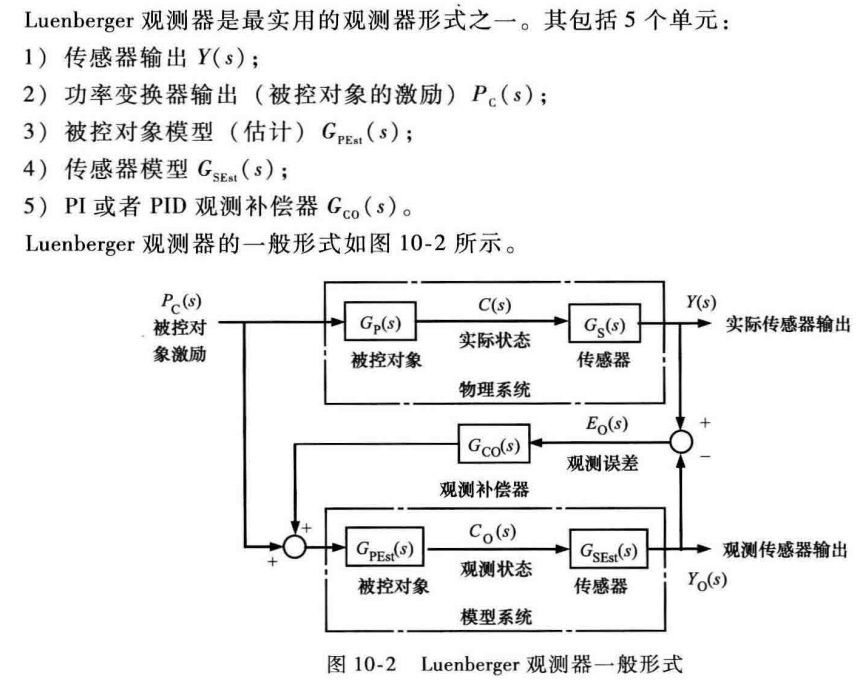
那么如何在一个传统控制系统中构建龙伯格观测器呢?

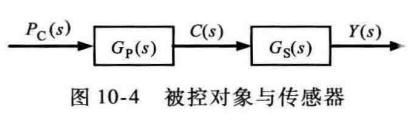
以上是一个典型的控制系统的结构图,理想情况下控制回路按照实际状态C(s)执行反馈,但实际情况当中常常需要传感器测量产生反馈变量y(s),再执行反馈,由传感器产生的典型问题是相位滞后、衰减和噪声,这些问题可能是由外界干扰、传感器的物理结构或者传感器自带的滤波器引起的。
我们可以直接的看出,理想的传感器的传递函数应该是等于1,换句话说,龙伯格观测器的第一个作用就是将传感器的传递函数不等于1所带来的影响最小化
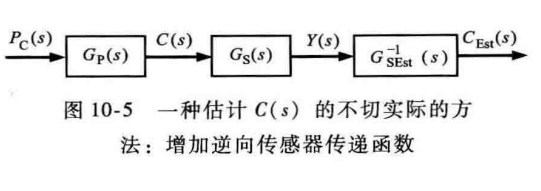
一种方法是在传感器信号之后,紧跟一个逆向传感器传递函数,从理论上来讲这种方案是可行的,但是在现实中往往难以求出传感器传递函数的逆。
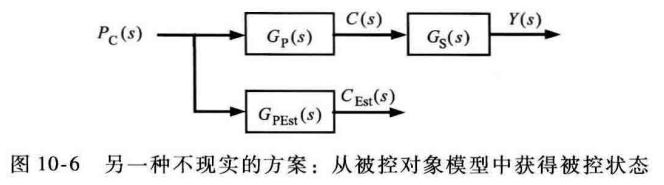
另一种方法则是用软件仿真被控对象的模型作为正在执行的控制回路,功率变换器输出的信号同时作用于实际被控对象和被控对象估计模型,也能够得到一个信号,但是由于大部分控制系统的被控对象中至少含有一个积分器,这样的解决方案容易受到漂移的影响也是不实用的。
但这两种方法也给我们带来了一些启示,我们可以构建类似于下面这种结构
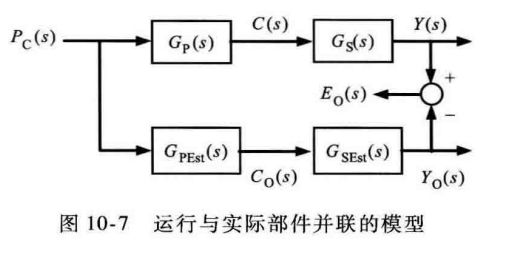
接收到来自功率变换的输出信号后,通过被控对象的模型和传感器的模型产生观测的传感器输出Y0,暂且假定该模型是实际部件的准确模型,此时我们得到的Y0就等于实际传感器所得到的数据ys,即图中的E0S等于零,而我们得到的观测状态C0S就是实际状态的准确表示。这种结构适用于模型可以完美表示实际被控对象的情况,
实际应用中,往往找不到完美描述实际被控对象的一种模型,也就是说在大多数情况下,图中的E0s不等于零,我们可以运用控制理论中经常提到的反馈的观点,就可以把误差信号E0s引入,模型当中形成一个反馈,最后使得E0s趋于0,此时得到的观察状态C0S就等于了实际状态CS
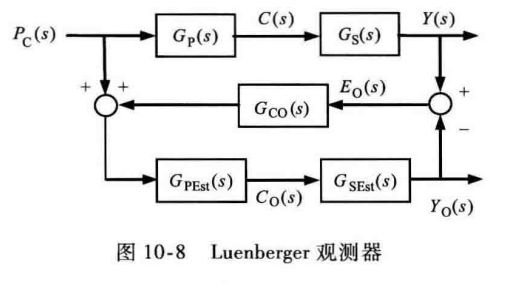
这种结构就是著名的龙伯格观测器,而在工程应用中,我们往往使用龙伯格观测器的滤波器形式,因涉及到数学公式推导,篇幅有限,这里不做介绍,见附录书籍的126-129页
重新审视龙伯格观测器的结构,重点在于如何确定被控对象的估计器,传感器的估计器和观测器补偿器的具体形式?
首先对于传感器的估计器来说,要重点考虑的就是传感器的比例增益,因为传感器比例增益的误差直接反映在观察状态里,我们依据厂商的数据,做出适当的努力,就可以建立这些装置的模型,在使用龙伯格观测器的滤波器形式时,可以简单的将传递将传感器选为低通滤波器,这样对于设计它的估计器就变得十分方便
对于被控对象的估计器来说,我们要重点关注的是比例增益、积分的阶次,和它的滤波作用,对于被控对象的增益来讲,它可能依赖于多个元件,并且可能随时变化,这给估计造成了一些困难,可以通过实验的方法逐步确定增益。大多数控制系统中被控对象具有一阶积分作用,因此我们也需要知道被控对象的阶次,而在估计完比例增益和积分作用之后,被控对象中所留下的就是关于滤波的影响了,和传感器一样,被控对象的滤波作用,一般可以由生产商的数据来确定,在大多数情况下这种滤波作用比较小。
对于观测器补偿器的设计来说,主要是选出哪种争议可用于补偿器的过程,在工程中,在这一环节中,一般采用PI或PID补偿器,对于较为简单的被控对象和传感器来说,PID补偿器已经足够了
参考链接:https://zhuanlan.zhihu.com/p/129732436
2、状态空间下龙伯格观测器设计
已经线性系统模型如下:
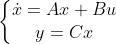
当系统状态量难以获取,但实际控制中又需要利用系统状态量时,如何通过输入量和输出量重构系统状态量?这便是龙伯格状态观测器设计初衷,将实现系统状态的系统称为状态观测器。
为确保估计状态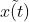 逼近系统真实状态
逼近系统真实状态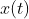 ,需满足如下条件:
,需满足如下条件:
![\lim_{t \to\propto }\left [{ \tilde x(t)-x(t)} \right ]=0](https://private.codecogs.com/gif.latex?%5Clim_%7Bt%20%5Cto%5Cpropto%20%7D%5Cleft%20%5B%7B%20%5Ctilde%20x%28t%29-x%28t%29%7D%20%5Cright%20%5D%3D0)
其中,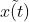 称为
称为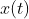 的重构状态或者状态估计值。
的重构状态或者状态估计值。
2.1 状态观测器设计
假设系统状态观测量和输出观测量满足如下方程:
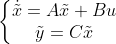
龙伯格状态观测器模型:
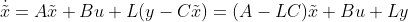
其中,A为状态矩阵,B为输入矩阵,C为输出矩阵,L为观测器增益矩阵,对偏差的加权。
若采用开环控制实现状态估计,其系统结构如图1所示,该系统模型简单,但存在模型不确定性和扰动,初始状态未知等问题。
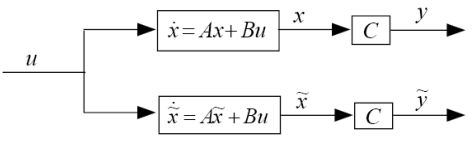
图1 基于开环控制的状态观测器实现
为提高系统的抗干扰性能,故采用闭环控制来实现状态估计,根据输出误差控制状态误差,使得估计状态和真实状态之间的误差逐步减小,其系统结构图如图2所示。

图2 基于闭环控制的状态观测器实现
定义真实状态和估计状态的误差向量如下:
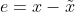
则误差的动态行为为:
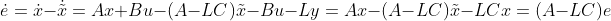
由上式可知,矩阵(A-LC)的极点决定了误差是否衰减以及如何衰减,而对于一个已知系统,A和C由系统特性决定。因此,增益矩阵L成为系统是否稳定的关键,这一问题被成为系统的极点配置问题。若能使得矩阵 A - LC 具有适当的特征值,则可以使得误差具有一定的衰减率。
由于
![det\left [ \lambda I-(A-LC) \right ]=det\left [ \lambda I-(A-LC)^{T} \right ]=det\left [ \lambda I-(A^{T}-C^{T}L^{T})\right ]](https://private.codecogs.com/gif.latex?det%5Cleft%20%5B%20%5Clambda%20I-%28A-LC%29%20%5Cright%20%5D%3Ddet%5Cleft%20%5B%20%5Clambda%20I-%28A-LC%29%5E%7BT%7D%20%5Cright%20%5D%3Ddet%5Cleft%20%5B%20%5Clambda%20I-%28A%5E%7BT%7D-C%5E%7BT%7DL%5E%7BT%7D%29%5Cright%20%5D)
因此,问题转化为 的极点配置问题,该极点配置问题可解的充要条件为:
的极点配置问题,该极点配置问题可解的充要条件为:
 完全能控
完全能控 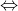
 完全能观
完全能观
观测器的增益矩阵可以按照极点配置方法来设计求解 的极点配置问题,得到增益矩阵K;观测器增益矩阵
的极点配置问题,得到增益矩阵K;观测器增益矩阵 。观测器设计的三种方法:直接法、变换法、爱克曼公式。
。观测器设计的三种方法:直接法、变换法、爱克曼公式。
3. 状态观测器实例
考虑由以下系数矩阵给定的系统
 ,
,  ,
, 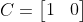
设计一个观测器,使观测器两个极点都是-2。
3.1 直接法
解:(1)检验系统的能观性:
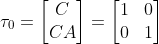
系统是能观的,因此问题可解。
(2) 要求确定观测器增益矩阵 ,使得矩阵
,使得矩阵 具有两个相同的特征值-2。由于
具有两个相同的特征值-2。由于
![det[\lambda I-(A-LC)]=det\left ( \begin{bmatrix} \lambda & 0\\ 0&\lambda \end{bmatrix} -\begin{bmatrix} 0 &1 \\ -1&0 \end{bmatrix}+\begin{bmatrix} l_{1}\\ l_{2} \end{bmatrix}\begin{bmatrix} 1 & 0 \end{bmatrix}\right ) \\ =det\left ( \begin{bmatrix} \lambda + l_{1} &-1 \\ 1+l_{2}& \lambda \end{bmatrix} \right ) \\ =\lambda ^{2}+l_{1}\lambda +1+l_{2}](https://private.codecogs.com/gif.latex?det%5B%5Clambda%20I-%28A-LC%29%5D%3Ddet%5Cleft%20%28%20%5Cbegin%7Bbmatrix%7D%20%5Clambda%20%26%200%5C%5C%200%26%5Clambda%20%5Cend%7Bbmatrix%7D%20-%5Cbegin%7Bbmatrix%7D%200%20%261%20%5C%5C%20-1%260%20%5Cend%7Bbmatrix%7D+%5Cbegin%7Bbmatrix%7D%20l_%7B1%7D%5C%5C%20l_%7B2%7D%20%5Cend%7Bbmatrix%7D%5Cbegin%7Bbmatrix%7D%201%20%26%200%20%5Cend%7Bbmatrix%7D%5Cright%20%29%20%5C%5C%20%3Ddet%5Cleft%20%28%20%5Cbegin%7Bbmatrix%7D%20%5Clambda%20+%20l_%7B1%7D%20%26-1%20%5C%5C%201+l_%7B2%7D%26%20%5Clambda%20%5Cend%7Bbmatrix%7D%20%5Cright%20%29%20%5C%5C%20%3D%5Clambda%20%5E%7B2%7D+l_%7B1%7D%5Clambda%20+1+l_%7B2%7D)
(3)期望的特征值多项式是
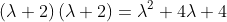
比较两个多项式,可以得到,
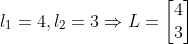
所求的观测器是
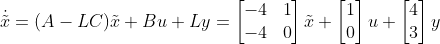
4、控制器与观测器对比
4.1 基于状态反馈的控制器设计
状态反馈是将系统的每一个状态变量乘以相应的反馈系数,然后反馈到输入端与参与输入相加形成控制律,作为受控系统的控制输入。图1是一个多输入—多输出系统状态反馈的基本结构。
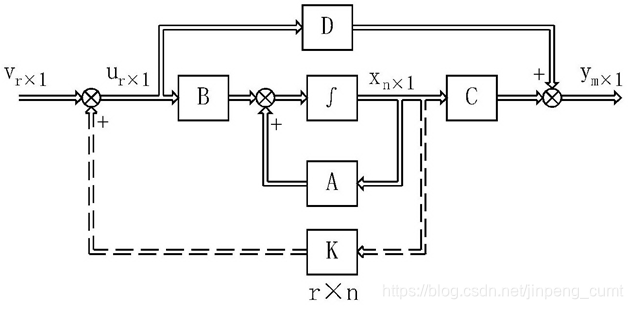
图1 多输入多输出系统状态反馈结构图
系统状态方程如下:
 (1)
(1)
式中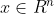 ;
;  ;
; ;
; 、
、 、
、 、
、 。若
。若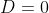 ,则受控系统简化为:
,则受控系统简化为:
 (2)
(2)
简记为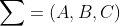
状态线性反馈控制律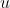 为
为
 (3)
(3)
其中, 维参考输入,
维参考输入, 维状态反馈系数阵或状态反馈增益阵。对单输入系统,
维状态反馈系数阵或状态反馈增益阵。对单输入系统,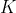 为
为 维行向量。
维行向量。
将(3)式代入(1)式整理可得状态反馈闭环系统的状态空间表达式如下:
 (4)
(4)
如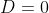 ,则
,则
 (5)
(5)
简记为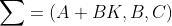
闭环系统的传递函数矩阵为
![W_{k}(s)=C[sI-(A+BK)]^{-1}B](https://private.codecogs.com/gif.latex?W_%7Bk%7D%28s%29%3DC%5BsI-%28A+BK%29%5D%5E%7B-1%7DB) (6)
(6)
比较开环系统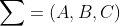 与闭环系统
与闭环系统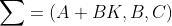 可见,状态反馈阵
可见,状态反馈阵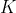 的引入,并不增加系统的维数,但可通过
的引入,并不增加系统的维数,但可通过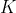 的选择自由地改变闭环系统的特征值,从而使系统获得所要求的性能。
的选择自由地改变闭环系统的特征值,从而使系统获得所要求的性能。
4.2 基于输出反馈的控制器设计
输出反馈是采用输出矢量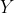 构成线性反馈律。在经典控制理论中主要讨论这种反馈形式。图2示出多输入—多输出系统输出反馈的基本结构。
构成线性反馈律。在经典控制理论中主要讨论这种反馈形式。图2示出多输入—多输出系统输出反馈的基本结构。

图2 多输入多输出系统输出反馈结构图
系统状态方程如下:
 (7)
(7)
输出线性反馈控制律为
 (8)
(8)
式中, 维输出反馈增益阵。对单输出系统,
维输出反馈增益阵。对单输出系统,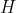 为
为 维列向量。闭环系统状态空间表达式可由式(7)代入(8)得:
维列向量。闭环系统状态空间表达式可由式(7)代入(8)得:
 (9)
(9)
整理得 :
 (10)
(10)
再把式(10)代入式(7)求得
![\left\{\begin{matrix} \dot{x}=[A+B(I-HD)^{-1}HC]x+B(I-HD)^{-1}v\\ y = [C+D(I-Hu)^{-1}HC]x+D(I-HD)^{-1}v \end{matrix}\right.](https://private.codecogs.com/gif.latex?%5Cleft%5C%7B%5Cbegin%7Bmatrix%7D%20%5Cdot%7Bx%7D%3D%5BA+B%28I-HD%29%5E%7B-1%7DHC%5Dx+B%28I-HD%29%5E%7B-1%7Dv%5C%5C%20y%20%3D%20%5BC+D%28I-Hu%29%5E%7B-1%7DHC%5Dx+D%28I-HD%29%5E%7B-1%7Dv%20%5Cend%7Bmatrix%7D%5Cright.) (11)
(11)
若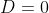 ,则
,则
 (12)
(12)
简记 。由式(12)可见,通过选择输出反馈增益阵
。由式(12)可见,通过选择输出反馈增益阵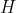 也可以改变闭环系统的特征值,从而改变系统的控制特性。
也可以改变闭环系统的特征值,从而改变系统的控制特性。
输出反馈系统的传递函数矩阵为
![W_{H}(s)=C[sI-(A+BHC)]^{-1}B](https://private.codecogs.com/gif.latex?W_%7BH%7D%28s%29%3DC%5BsI-%28A+BHC%29%5D%5E%7B-1%7DB) (13)
(13)
若受控系统的传递函数阵为
![W_{0}(s)=C[sI-A]^{-1}B](https://private.codecogs.com/gif.latex?W_%7B0%7D%28s%29%3DC%5BsI-A%5D%5E%7B-1%7DB) (14)
(14)
则 和
和 存在下列关系
存在下列关系
![W_{H}(s)=W_{0}(s)[I-HW_{0}(s)]^{-1}](https://private.codecogs.com/gif.latex?W_%7BH%7D%28s%29%3DW_%7B0%7D%28s%29%5BI-HW_%7B0%7D%28s%29%5D%5E%7B-1%7D) (15)
(15)
或者
![W_{H}(s)=[I-W_{0}(s)H]^{-1}W_{0}(s)](https://private.codecogs.com/gif.latex?W_%7BH%7D%28s%29%3D%5BI-W_%7B0%7D%28s%29H%5D%5E%7B-1%7DW_%7B0%7D%28s%29) (16)
(16)
比较上述两种基本形式的反馈可以看出,输出反馈中的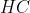 与状态反馈中的
与状态反馈中的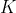 相当。但由于
相当。但由于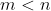 ,所以
,所以 可供选择的自由度远比
可供选择的自由度远比 小,因而输出反馈只能相当于一部分状态反馈。只有当
小,因而输出反馈只能相当于一部分状态反馈。只有当 时,
时, 才能等同于全状态反馈。因此,在不增加补偿器的条件下,输出反馈的效果显然不如状态反馈系统好。但输出反馈在技术实现上的方便性则是其突出优点。
才能等同于全状态反馈。因此,在不增加补偿器的条件下,输出反馈的效果显然不如状态反馈系统好。但输出反馈在技术实现上的方便性则是其突出优点。
4.3. 基于观测器的控制器
系统模型
 (17)
(17)
假定系统是能控、能观的。使得闭环系统极点为 的状态反馈控制律是
的状态反馈控制律是 。若系统状态不能直接测量,可以利用龙伯格观测器来估计系统的状态。
。若系统状态不能直接测量,可以利用龙伯格观测器来估计系统的状态。
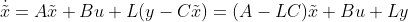 (18)
(18)
进而用 来替代原来的控制。
来替代原来的控制。
将 代入(18)式,可得利用状态估计值的反馈控制器如下:
代入(18)式,可得利用状态估计值的反馈控制器如下:
 (19)
(19)
基于观测器的输出反馈控制系统结构图3所示:
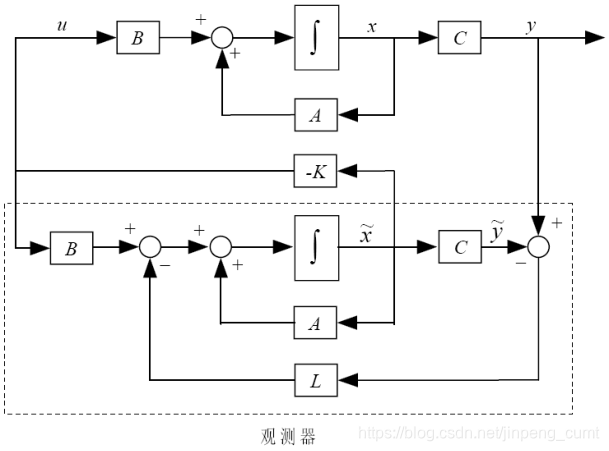
图3 基于观测器的状态反馈控制系统结构
由图3可知,系统增加了积分器,闭环系统是2n 阶的。
(1)若选择 为闭环系统状态,则系统状态方程
为闭环系统状态,则系统状态方程
 (20)
(20)
 (21)
(21)
写成矩阵向量形式:
 (22)
(22)
定义误差向量: ,则
,则
 (23)
(23)
其特征多项式为
![det\left [ \lambda I-(A-LC) \right ]=det\left [ \lambda I-(A-LC)^{T} \right ]=det\left [ \lambda I-(A^{T}-C^{T}L^{T})\right ]](https://private.codecogs.com/gif.latex?det%5Cleft%20%5B%20%5Clambda%20I-%28A-LC%29%20%5Cright%20%5D%3Ddet%5Cleft%20%5B%20%5Clambda%20I-%28A-LC%29%5E%7BT%7D%20%5Cright%20%5D%3Ddet%5Cleft%20%5B%20%5Clambda%20I-%28A%5E%7BT%7D-C%5E%7BT%7DL%5E%7BT%7D%29%5Cright%20%5D) (24)
(24)
(2)若选择 为闭环系统状态,则系统状态方程
为闭环系统状态,则系统状态方程
 (25)
(25)
其特征多项式为
 (26)
(26)
分离性原理 闭环系统的极点是极点配置单独设计产生的极点和由观测器单独设计产生的极点两部分组成。
本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有涉嫌抄袭侵权的内容,请联系:hwhale#tublm.com(使用前将#替换为@)