注意,本文内容来自于吴恩达老师cs229课堂笔记的中文翻译项目:https://github.com/Kivy-CN/Stanford-CS-229-CN 中的凸优化部分的内容进行翻译学习。
3. 凸函数
凸优化的一个核心要素是凸函数的概念。
定义
3.1
3.1
3.1 我们称一个函数
f
:
R
n
→
R
f:R^n\rightarrow R
f:Rn→R是一个凸函数,需要满足其定义域(记作
D
(
f
)
\mathcal{D}(f)
D(f))是一个凸集,同时给定任意
x
,
y
∈
D
(
f
)
x,y\in \mathcal{D}(f)
x,y∈D(f)以及
θ
∈
R
,
0
≤
θ
≤
1
\theta\in R,0\le\theta\le 1
θ∈R,0≤θ≤1,满足:
f
(
θ
x
+
(
1
−
θ
)
y
)
≤
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
f(\theta x +(1-\theta) y)\le \theta f(x)+(1-\theta)f(y)
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)
(译者注:注意这里函数的凸凹性和我们本科《高等数学》上册里面微分中值定理与导数应用章节中曲线的凸凹性是相反的,不过这里定义的凸凹的方向在机器学习中更常见)
直观地,考虑这个定义的方法是如果我们在凸函数的图上取任意两点并在两点之间画一条直线,那么函数在这两点之间的部分就会在这条直线下面。这种情况如图
2
2
2^2
22所示。
2 不要太担心
f
f
f的定义域是凸集的要求,这个要求仅仅是在技术上保证
f
(
θ
x
+
(
1
−
θ
)
y
)
f(\theta x +(1-\theta) y)
f(θx+(1−θ)y)有定义(如果定义域
D
(
f
)
\mathcal{D}(f)
D(f)不是凸集,则即使
x
,
y
∈
D
(
f
)
x,y\in\mathcal{D}(f)
x,y∈D(f),
f
(
θ
x
+
(
1
−
θ
)
y
)
f(\theta x +(1-\theta) y)
f(θx+(1−θ)y)也有可能没有意义)
如果在定义
3.1
3.1
3.1的基础上增加严格的不等的条件
x
≠
y
x\ne y
x̸=y和
0
<
θ
<
1
0<\theta<1
0<θ<1,则可以说一个函数是严格凸函数。如果
f
f
f是凸函数则我们可以得到
−
f
-f
−f是凹函数, 同理如果
f
f
f是严格凸函数则
−
f
-f
−f是严格凹函数。

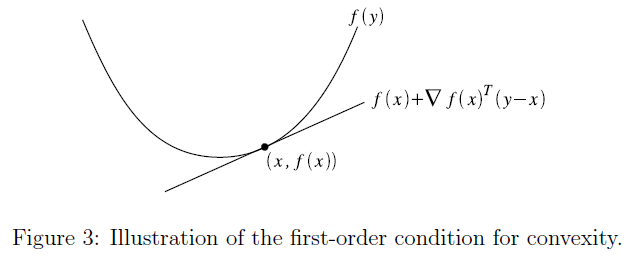
3.1 凸性的一阶条件
假设函数
f
:
R
n
→
R
f:R^n\rightarrow R
f:Rn→R可微(即其梯度
3
∇
x
f
(
x
)
^3\nabla_xf(x)
3∇xf(x)在函数
f
f
f的定义域内处处存在)。则
f
f
f是一个凸函数,只要满足
D
(
f
)
\mathcal{D}(f)
D(f)是一个凸集,同时对所有的
x
,
y
∈
D
(
f
)
x,y\in\mathcal{D}(f)
x,y∈D(f),有:
3 回忆一下梯度定义为
∇
x
f
(
x
)
∈
R
n
,
(
∇
x
f
(
x
)
)
i
=
∂
f
(
x
)
∂
x
i
\nabla_xf(x)\in R^n,(\nabla_xf(x))_i=\frac{\partial f(x)}{\partial x_i}
∇xf(x)∈Rn,(∇xf(x))i=∂xi∂f(x)。有关梯度和海森函数的知识,请参阅前面关于线性代数的部分的章节笔记。
f
(
y
)
≥
f
(
x
)
+
∇
x
f
(
x
)
T
(
y
−
x
)
f(y)\ge f(x)+\nabla_xf(x)^T(y-x)
f(y)≥f(x)+∇xf(x)T(y−x)
函数
f
(
x
)
+
∇
x
f
(
x
)
T
(
y
−
x
)
f(x)+\nabla_xf(x)^T(y-x)
f(x)+∇xf(x)T(y−x)称为函数
f
(
x
)
f(x)
f(x)在点
x
x
x处的一阶近似(first-order approximation)。 直觉上来说,这个函数可以近似的认为是函数
f
f
f在点
x
x
x处的切线。凸性的一阶条件就是阐明了,
f
f
f是凸函数当且仅当该函数的切线是一个全局下估计(global underestimator)。换句话说,如果我们根据函数的特性在任意一点绘制该函数的切线,那么这条直线上的每一点将低于函数
f
f
f在相应位置的点。
与凸性的定义类似,当严格不等条件成立时
f
f
f是严格凸函数,当不等式符号颠倒时
f
f
f是凹函数,当颠倒的不等式的严格不等条件成立时
f
f
f是严格凹函数。
3.2 凸性的二阶条件
假设函数
f
:
R
n
→
R
f:R^n\rightarrow R
f:Rn→R二阶可微(即其海森矩阵
4
∇
x
2
f
(
x
)
^4\nabla_x^2f(x)
4∇x2f(x)在函数
f
f
f的定义域内处处存在)。则
f
f
f是一个凸函数,只要满足
D
(
f
)
\mathcal{D}(f)
D(f)是一个凸集,同时对所有的
x
,
y
∈
D
(
f
)
x,y\in\mathcal{D}(f)
x,y∈D(f),有:
4 回忆一下海森矩阵定义为
∇
x
2
f
(
x
)
∈
R
n
×
n
,
(
∇
x
2
f
(
x
)
)
i
j
=
∂
2
f
(
x
)
∂
x
i
∂
x
j
\nabla_x^2f(x)\in R^{n\times n},(\nabla_x^2f(x))_{ij}=\frac{\partial^2 f(x)}{\partial x_i\partial x_j}
∇x2f(x)∈Rn×n,(∇x2f(x))ij=∂xi∂xj∂2f(x)
∇
x
2
f
(
x
)
⪰
0
\nabla_x^2f(x)\succeq 0
∇x2f(x)⪰0
当符号“
⪰
\succeq
⪰”在这里与矩阵结合使用时,指的是正半定矩阵,而不是分量不等式(componentwise inequality)
5
^5
5。在一维中,这等价于二阶导数
f
′
′
(
x
)
f''(x)
f′′(x)总是非负的(即函数始终为绝对的非负值(positive non-negative))。
5 与对称矩阵
X
∈
S
n
X\in S^n
X∈Sn类似,
X
⪯
0
X\preceq 0
X⪯0代表
X
X
X是负定矩阵。对于向量不等式来说,有时可以用符号‘
≤
\le
≤’和‘
≥
\ge
≥’代替符号‘
⪯
\preceq
⪯’和‘
⪰
\succeq
⪰’。尽管这里的符号类似向量的符号,但是意义非常不一样。特别的,矩阵
X
⪰
0
X\succeq 0
X⪰0并不意味着对于所有矩阵的元素下标
i
,
j
i,j
i,j都有元素
X
i
j
≥
0
X_{ij}\ge 0
Xij≥0
同样,与凸性的定义以及一阶条件类似,如果海森矩阵是正定的,则函数
f
f
f是严格凸函数,如果是半负定则函数是凹函数,是负定则函数是严格凹函数。
3.3 Jensen不等式
假设我们从凸函数的基本定义中的不等式开始:
f
(
θ
x
+
(
1
−
θ
)
y
)
≤
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
其
中
0
≤
θ
≤
1
f(\theta x +(1-\theta) y)\le \theta f(x)+(1-\theta)f(y)\quad 其中\quad 0\le\theta\le 1
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)其中0≤θ≤1
使用归纳法,这可以相当容易地扩展到多个点的凸组合:
f
(
∑
i
=
1
k
θ
i
x
i
)
≤
∑
i
=
1
k
θ
i
f
(
x
i
)
其
中
∑
i
=
1
k
θ
i
=
1
,
θ
i
≥
0
∀
i
f(\sum_{i=1}^k\theta_ix_i)\le\sum_{i=1}^k\theta_if(x_i)\quad 其中\quad\sum_{i=1}^k\theta_i=1,\theta_i\ge 0\quad\forall i
f(i=1∑kθixi)≤i=1∑kθif(xi)其中i=1∑kθi=1,θi≥0∀i
事实上,这也可以推广到无穷和或积分。在后一种情况下,不等式可以写成:
f
(
∫
p
(
x
)
x
d
x
)
≤
∫
p
(
x
)
f
(
x
)
d
x
其
中
∫
p
(
x
)
x
d
x
=
1
,
p
(
x
)
≥
0
∀
i
f(\int p(x)xdx)\le\int p(x)f(x)dx\quad 其中\quad\int p(x)xdx=1,p(x)\ge0\quad\forall i
f(∫p(x)xdx)≤∫p(x)f(x)dx其中∫p(x)xdx=1,p(x)≥0∀i
由于
p
(
x
)
p(x)
p(x)积分为
1
1
1,通常把它看作概率密度,在这种情况下,前面的方程可以用期望来表示:
f
(
E
[
x
]
)
≤
E
[
f
(
x
)
]
f(E[x])\le E[f(x)]
f(E[x])≤E[f(x)]
最后一个不等式叫做Jensen不等式,后面的课上会讲到。
6
^6
6
6 事实上,这四个方程有时都被称为Jensen不等式,因为它们都是等价的。但是,对于这门课,我们将使用该术语来具体指这里给出的最后一个不等式。
3.4 水平集
凸函数产生一种特别重要的凸集称为
α
−
s
u
b
l
e
v
e
l
\alpha-sublevel
α−sublevel集。 给出了凸函数
f
:
R
n
→
R
f:R^n\rightarrow R
f:Rn→R和一个实数
α
∈
R
\alpha\in R
α∈R,
α
−
s
u
b
l
e
v
e
l
\alpha-sublevel
α−sublevel集被定义为:
{
x
∈
D
(
f
)
:
f
(
x
)
≤
α
}
\{x\in\mathcal{D}(f):f(x)\le\alpha\}
{x∈D(f):f(x)≤α}
换句话说,
α
−
s
u
b
l
e
v
e
l
\alpha-sublevel
α−sublevel集是所有满足
f
(
x
)
≤
α
f(x)\le\alpha
f(x)≤α的点
x
x
x的集合。
为了证明这是一个凸集,考虑任意
x
,
y
∈
D
(
f
)
x,y\in\mathcal{D}(f)
x,y∈D(f),并且
f
(
x
)
≤
α
,
f
(
y
)
≤
α
f(x)\le\alpha,f(y)\le\alpha
f(x)≤α,f(y)≤α,则:
f
(
θ
x
+
(
1
−
θ
)
y
)
≤
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
≤
θ
α
+
(
1
−
θ
)
α
=
α
f(\theta x +(1-\theta) y)\le \theta f(x)+(1-\theta)f(y)\le\theta\alpha+(1-\theta)\alpha=\alpha
f(θx+(1−θ)y)≤θf(x)+(1−θ)f(y)≤θα+(1−θ)α=α
3.5 凸函数判断的实例
我们从几个单变量凸函数的简单例子开始,然后继续讨论多元函数。
-
指数函数是凸函数。有函数
f
:
R
→
R
f:R\rightarrow R
f:R→R,任意
a
∈
R
a\in R
a∈R使得
f
(
x
)
=
e
a
x
f(x)=e^{ax}
f(x)=eax。为了证明
f
f
f是凸函数,我们可以简单的考虑二阶导数
f
′
′
(
x
)
=
a
2
e
a
x
f''(x)=a^2e^{ax}
f′′(x)=a2eax,对于所有
x
x
x都是正的。
-
负对数函数是凸函数。函数
f
:
R
→
R
,
f
(
x
)
=
−
l
o
g
x
f:R\rightarrow R,f(x)=-logx
f:R→R,f(x)=−logx,有定义域
D
(
f
)
=
R
+
+
\mathcal{D}(f)=R_{++}
D(f)=R++(这里的
R
+
+
R_{++}
R++代表严格正实数的集合
{
x
:
x
>
0
}
\{x:x>0\}
{x:x>0})。则对于所有的
x
x
x都满足
f
′
′
(
x
)
=
1
/
x
2
>
0
f''(x)=1/x^2>0
f′′(x)=1/x2>0。
-
仿射函数。函数
f
:
R
→
R
,
f
(
x
)
=
b
T
x
+
c
f:R\rightarrow R,f(x)=b^Tx+c
f:R→R,f(x)=bTx+c,满足
b
∈
R
n
,
c
∈
R
b\in R^n,c\in R
b∈Rn,c∈R。在这种情况下对于所有的
x
x
x,该函数的海森矩阵
∇
x
2
f
(
x
)
=
0
\nabla^2_xf(x)=0
∇x2f(x)=0。应为零矩阵即是半正定也是半负定矩阵,因此函数
f
f
f即是凸函数,也是凹函数。事实上,这种形式的仿射函数是唯一既凸又凹的函数。
-
二次函数。函数
f
:
R
→
R
,
f
(
x
)
=
1
2
x
T
A
x
+
b
T
x
+
c
f:R\rightarrow R,f(x)=\frac12x^TAx+b^Tx+c
f:R→R,f(x)=21xTAx+bTx+c,系数的对称矩阵为
A
∈
S
n
,
b
∈
R
n
A\in S^n,b\in R^n
A∈Sn,b∈Rn以及
c
∈
R
c\in R
c∈R。在先前线性代数笔记中,我们展示了这个函数的海森函数为:
∇
x
2
f
(
x
)
=
A
\nabla^2_xf(x)=A
∇x2f(x)=A
因此,函数
f
f
f的凸性或非凸性完全取决于A是否为半正定矩阵:如果
A
A
A为半正定,则函数为凸函数(严格凸、凹、严格凹函数同样类比);如果
A
A
A是不定的矩阵,那么
f
f
f既不是凸函数也不是凹函数。
注意,平方欧几里得范数
f
(
x
)
=
∥
x
∥
2
2
=
x
T
x
f(x) = \parallel x\parallel^2_2=x^Tx
f(x)=∥x∥22=xTx是二次函数的一个特例,其中
a
=
I
,
b
=
0
,
c
=
0
a = I, b = 0, c = 0
a=I,b=0,c=0,因此它是一个严格凸函数。
-
范数函数是凸函数。函数
f
:
R
→
R
f:R\rightarrow R
f:R→R为
R
n
R^n
Rn上的某个范数。然后根据三角不等式和正范数的同质性,对于
x
,
y
∈
R
n
,
0
≤
θ
≤
1
x,y\in R^n,0\le\theta\le 1
x,y∈Rn,0≤θ≤1,有:
f
(
θ
x
+
(
1
−
θ
)
y
)
≤
f
(
θ
x
)
+
f
(
(
1
−
θ
)
y
)
=
θ
f
(
x
)
+
(
1
−
θ
)
f
(
y
)
f(\theta x +(1-\theta) y)\le f(\theta x)+f((1-\theta)y) =\theta f(x)+(1-\theta)f(y)
f(θx+(1−θ)y)≤f(θx)+f((1−θ)y)=θf(x)+(1−θ)f(y)
这是一个凸函数的例子,由于范数不是处处可微的(例如,
1
1
1范数,
∥
x
∥
1
=
∑
i
=
1
n
∣
x
i
∣
\parallel x\parallel_1 = \sum_{i=1}^n|x_i|
∥x∥1=∑i=1n∣xi∣,在任意
x
i
=
0
x_i = 0
xi=0的点上都是不可微的),因此无法根据二阶或一阶条件证明凸性。
-
凸函数的非负加权和是凸函数。令
f
1
,
f
2
,
…
,
f
k
f_1,f_2,\dots,f_k
f1,f2,…,fk是凸函数,并且有
w
1
,
w
2
,
…
,
w
k
w_1,w_2,\dots,w_k
w1,w2,…,wk都是非负实数,则:
f
(
x
)
=
∑
i
=
1
k
w
i
f
i
(
x
)
f(x) = \sum_{i=1}^kw_if_i(x)
f(x)=i=1∑kwifi(x)
是一个凸函数,因为:
f
(
θ
x
+
(
1
−
θ
)
y
)
=
∑
i
=
1
k
w
i
f
i
(
θ
x
+
(
1
−
θ
)
y
)
≤
∑
i
=
1
k
w
i
(
θ
f
i
(
x
)
)
+
(
1
−
θ
)
f
i
(
y
)
)
=
θ
∑
i
=
1
k
w
i
f
i
(
x
)
+
(
1
−
θ
)
∑
i
=
1
k
w
i
f
i
(
y
)
=
θ
f
(
x
)
+
(
1
−
θ
)
f
(
x
)
\begin{aligned} f(\theta x +(1-\theta) y)&=\sum_{i=1}^kw_if_i(\theta x +(1-\theta) y) \\ &\le\sum_{i=1}^kw_i(\theta f_i(x))+(1-\theta)f_i(y)) \\ &=\theta\sum_{i=1}^kw_if_i(x)+(1-\theta)\sum_{i=1}^kw_if_i(y) \\ &=\theta f(x) + (1-\theta)f(x) \end{aligned}
f(θx+(1−θ)y)=i=1∑kwifi(θx+(1−θ)y)≤i=1∑kwi(θfi(x))+(1−θ)fi(y))=θi=1∑kwifi(x)+(1−θ)i=1∑kwifi(y)=θf(x)+(1−θ)f(x)
下一篇:凸优化学习(四)——凸优化问题