约束下的最优求解：拉格朗日乘数法和KKT条件

　　机器学习面对各种各样的求解极值或者最值问题 ，现在对常见的求解极值或者最值问题思路做一下理论上的梳理。

最值问题

简单了解最值问题

　　求最值是非常常见的问题，比如如何选择交通路线，最快地到达某地；如何用手头的钱买到分量最重的水果等等。
　　我们可以把需求定义为一个目标函数： f(x)
　　最值问题也就可以表示为 min[f(x)]
　　对于一个函数求解最值问题，我们要先查看函数的特性，比如是否单调，是否有拐点，是否有峰谷等。
　　比如，在可导时，利用导数函数是否大于0，来判断函数是否增减，并且令导数为0来找到极值点。
　　利用二阶导数是否大于0，来判断函数是否凹凸。

常见几种最值问题的形式

　　（1）

min/maxf(w)
　　（2） min/maxf(w)
　　 s.t.gi(w)=0,i=1,2,...,n
　　（3） min/maxf(w)
　　 s.t.gi(w)=0,i=1,2,...,n;
　　 hj(w)⩽0,j=1,2,...,m
　　整体思路，就是无约束最好解决，带约束的转化为无约束的问题再解决。

约束

　　上面说的是一般情况下，直接对函数求解最值。实际问题不会总是这么简单，还会有老多的限制的，比如我想省时间，还只花10元路费，那么该怎么选择路线；所买的商品单价不能小于15元，该怎么才能买到分量最多的水果。
　　在实际情形下，比如我们的逻辑回归，我们会加上惩罚项 12wTw ，得到新的目标函数：
　　

f(x)=Ferror+Fpenalty
　　效果是对权重进行了约束，而且这个权重是分布于0附近的，这个惩罚怎么解释呢。这是一个直接给出的结果，其实最本质的表示应该是:
　　 minFerror
　　在约束 wTw≤1 下
　对原来的误差函数进行最优化求解。于是才有了上面那个加入惩罚之后的目标函数。

约束下的最值问题

　　为什么会有上面的变换呢，可能大家还是一头雾水，为什么我在某个约束条件下求某个目标函数的最优解，就突然变成了最上面的新目标函数？
　　这个疑惑的解答要先从拉格朗日乘数法讲起。

拉格朗日乘数法

　　对于第二种形式，带约束条件的问题，我们更倾向于将其转化为无约束问题。在数学最优化问题中，拉格朗日乘数法是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题，其变量不受任何约束。这种方法引入了一种新的标量未知数，即拉格朗日乘数（：约束方程的梯度（gradient）的线性组合里每个向量的系数，搞不懂这句话在说神马）。
　　上面这段话读起来挺绕的，还是举个例子吧。
　　目标是求 f(x,y)=x2∗y 的最大值
　　同时满足 x2+y2=1
　　怎么将这两个式子凑到一起呢？引入个系数变量 λ
　　构造新目标函数 F(x,y,λ)=x2∗y+λ∗(x2+y2−1)
　　我们看看新目标函数的特点：
　　对 λ 求导，则得：（1） ∂f(x,y,λ)∂λ=x2+y2−1
　　对 x 求导，则得：（2）∂f(x,y,λ)∂x=2xy+2λx
　　对 y 求导，则得：（3）∂f(x,y,λ)∂y=x2+2λy
　　若是按照一个函数的最值存在于其极值的思想来解答，则令这三个式子为0，可以看到，原来的约束也包括进了新目标函数中，不过是引入了个新变量 λ 。
　　并且在 F(x,y,λ) 取得极值时，与 f(x,y) 相等，因为 F 取得极值时，∂f(x,y,λ)∂λ=x2+y2−1=0， F(x,y,λ) 变为 f(x,y) 。故， F(x,y,λ) 的极值必然是f(x, y)的极值。这段话很重要~
　　
　　但是这里对原参数的偏导数里多出来的 λ 项怎么解释呢？
　　 λ 的物理意义：表示原目标函数在约束下，所能达到的最大增长率（梯度）。其解释如下：
　　 F(w,λ)=f(w)+λ∗g(w) ;
　　 ∂F∂w=∂f∂w+λ∂g∂w ;
　　 ∂F∂λ=g(w)
　　令 ∂F∂w=0 ，则得 λ=−f′wg′w ，可以看出来原目标函数 f(w) 的的梯度（最大增长率）受到了 g(w) 的梯度约束。
　　若是将 ∂F∂λ=g(w)=0 带入上述 λ 式子中，可以得到在确定约束条件下的原目标函数的梯度。（这个说法有问题没有？上面 λ 式子已经是在极值下求解得到的，不过没有考虑约束 g(x)=0 ，所以这个说法是没问题的）
　　（因此，上面的求解最优值，就变成了在约束条件下，原目标函数在约束函数下的梯度求解问题。怎么感觉怪怪的，没想到就变成了这样的问题。错误原因：有地方理解的有问题，对新目标求极值，中间找到了参数间的关系，然后把一个变量表示了出来，只能说明新目标函数在极值时的某个参数的样子）
　　
　　画个图或许更直观一些。
　　在约束条件下某目标函数的最值，只可能出现在约束函数的等高线和目标函数在参数面投影的相切的地方。
　　

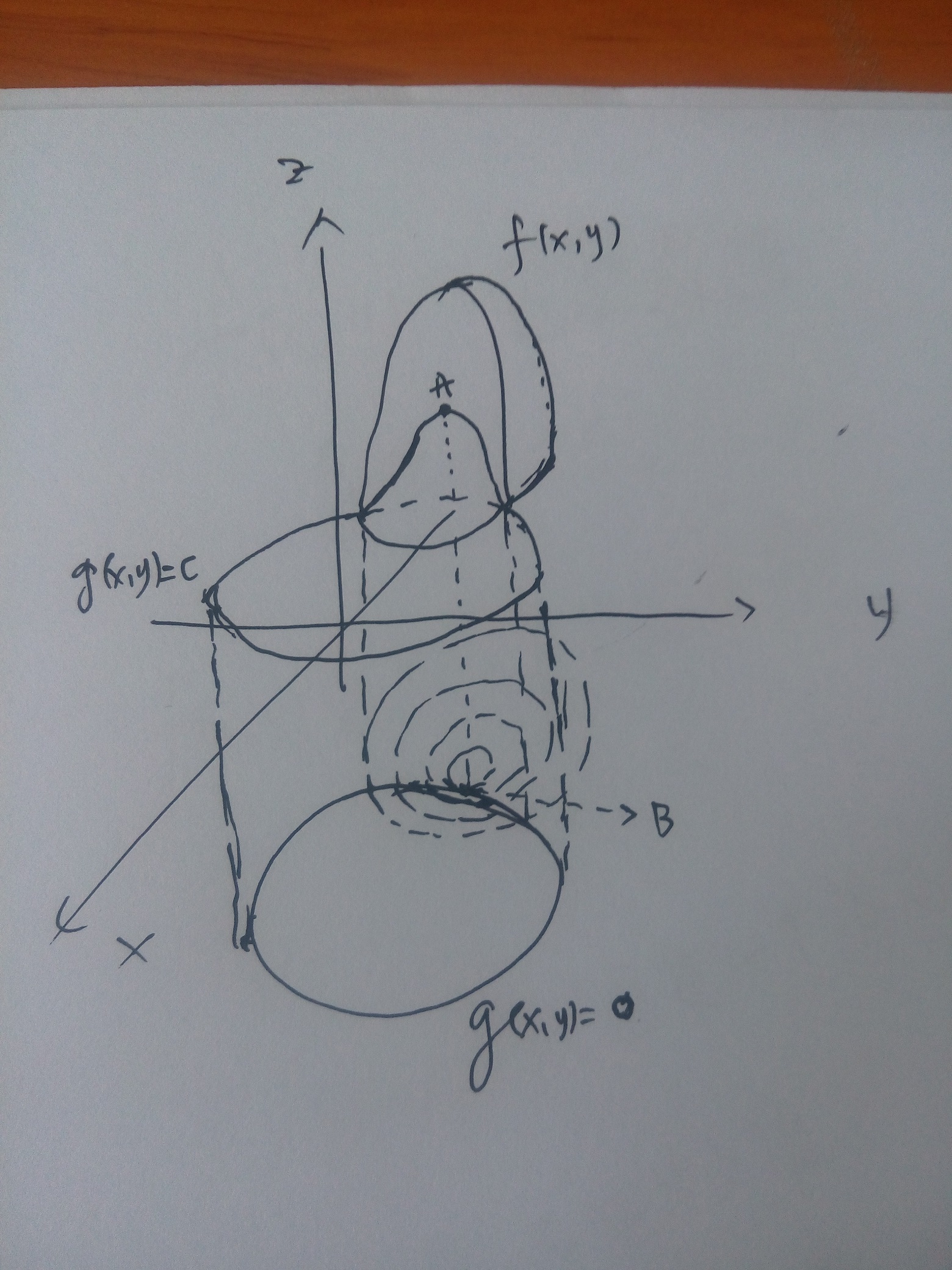
　　上图中， f(x,y) 为目标函数， g(x,y)=c 为约束条件，我们将两者投影到 xy 平面上得到两者的等高线分布，体现在空间中就是 g(x,y)=0 向上做垂直切面，切割了 f(x,y) ，得到了个曲线，这个曲线投影到 xy 面上刚好与 g(x,y)=0 重合，可以看到随着 f(x,y) 的 xy 范围缩小（对应其值逐渐增大），会有个与 g(x,y)=0 的切点B，对应于 f(x,y) 上的A点。A点则是满足约束的，刚好又是最值的地方。

对逻辑回归里惩罚的解释

　　现在回过头来看，线性回归目标函数里面的惩罚，是怎么个情况，明白了没？结果发现还是没能够解释为什么要加惩罚 12wTw 。哎~！~好囧~！~
　　经过跟马博和贾老师的讨论，终于把这个问题整出了一个较为合理的解释。
　　首先高次多项式回归的评估函数是误差函数：
　　 cost(x,w)=12∑Mi=1[f(x,w)−y]2 ；前面的1/2是为了后期求导的时候方便。
　　现在对参数 w 进行约束，因为高次对应的参数会很大程度上影响拟合度，并且会有甩尾现象，想把其影响降到较小程度，并且尽可能保留主要部分（w0对应的信息）使得泛化能力强，我们想怎么去约束 w 呢？
　　如果wT∗w⩽w20（二阶范数约束，肯定还有其他约束的情况），那岂不是实现了我们的约束目的，一方面对高次对应的参数进行了约束，一方面他们对整体的影响还不会对整体超过 w0 的影响。
　　这样，还不能够用拉格朗日乘子法，因为该方法是解决等式约束的最值问题。怎么办呢？好好看看误差函数，这是一个凸函数，我们对 w 的约束是在某个范围内，那么根据上面手绘图来看，最值的解只可能出现在，误差函数的等高线与约束最外边缘的切点上。啊哈，这个地方给了我们很大启示，可以直接在约束边缘上找到误差函数的最小值即可。
　　看下面这个图，就很直观地说明了这个问题。左侧为二阶范数约束，右侧为一阶范数约束。
　　
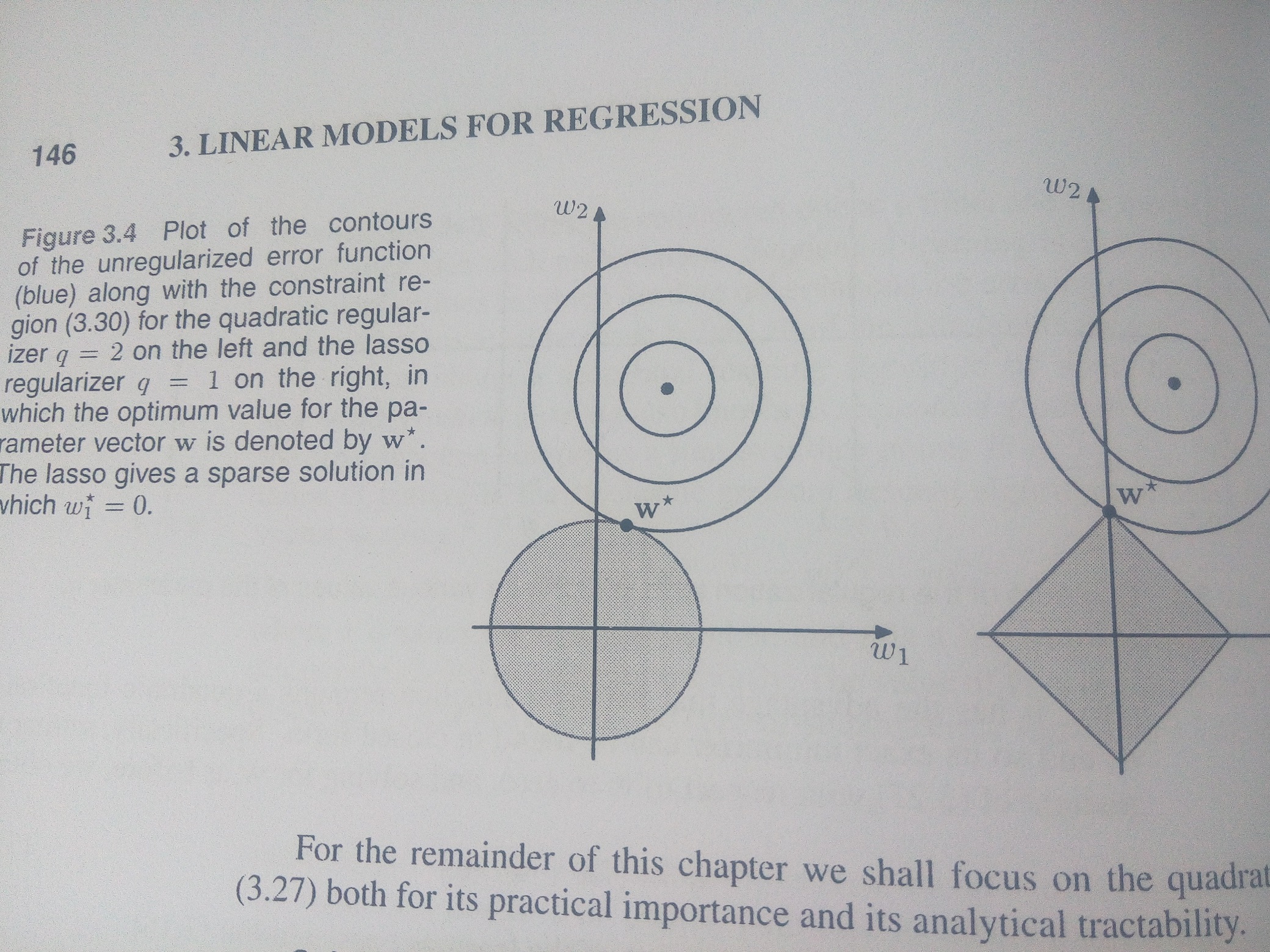
　　于是对误差函数的在不等式wTw⩽w20的最值问题的解，就是误差函数在等式 wTw=w20 的最值的解。
　　哈哈，终于可以正大光明的应用拉格朗日乘子法了，于是就有了我们加入惩罚之后的新的代价函数：
　　 Cost(x,w)=∑Mi=1[f(x,w)−y]2+λ[wT∗w−w20]
　　这地方离着我们在书本上看到的代价函数还有点区别，就是 λ 向量统一变成了 12 ，目测估计是为了方便求解。
　　可以有其他的约束，比如 ∑Mj=0|wj|q⩽η

KKT条件下最优求解

　　对于第三种情况，又有等式约束，又有不等式约束的，怎么搞呢？上面我们是用拉格朗日乘数法搞定的等式约束的问题，那么对于包括有不等式约束的，可不可以把拉格朗日乘数法扩展一下，充分利用它，解决现在的问题呢？答案是可以，就是满足KKT条件时的最值求解。
　　KKT条件：在满足一些有规则的条件下，一个非线性规划（Nonlinear Programming）问题能有最优化解的一个必要和充分条件。这是一个广义化拉格朗日乘数的成果，KKT是三个作者的首字母，Karush & Kuhn &Tucker。
　　求解的问题是：
　　

minf(w)
　　 s.t.gi(w)=0,i=1,2,...,n;
　　 hj(w)⩽0,j=1,2,...,m;
　　什么条件下，上述问题有最值解呢？
　　KKT出场了~
　　先说 充分条件：
　　如果有常数 μi⩾0 及 vj 满足下述条件：
　　 ▽f(w)+∑ni=1μi▽gi(w)+∑mj=1vj▽hj(w)=0
　　且 μigi(w)=0 for all i=1,2,...,n
　　当然有个重要的前提假设，就是目标函数 f 和约束函数g都是凸函数。
　　再说 必要条件：
　　如果目标函数和约束函数在某点 w 连续可微，点w为一局部极小值，那么则存在一组所称乘子的常数 λ⩾0, μi⩾0(i=1,2,3,...,n) 及 vj(j=1,2,...,m) 满足如下条件：
　　 λ+∑ni=1μi+∑mj=1|vj|>0
　　 λ▽f(w)+∑ni=1μi▽gi(w)+∑mj=1vj▽hj(w)=0
　　 μigi(w)=0 for i=1,2,...,n
　　那么这个点 w 是全局最小值。（▽都是对参数 w <script type="math/tex" id="MathJax-Element-93">w</script>求导）

小结

　　约束下的函数最值问题求解，即将约束问题转化为无约束问题，然后再去解决。
　　中间会有一些小技巧，自己需要在实际应用中灵活应变。