术语
- 图——由结点的有穷集合V和边的集合E组成,在图中,结点常被称为顶点,若两个顶点之间存在一条边,则表示两个顶点相邻。
- 有向图——图的每条边都有方向。
- 无向图——图的每条边没有方向。
- 弧——有向图中,常将边称为弧,含箭头的一端称为弧头,另一端称为弧尾,记作 <
v
i
,
v
j
v_i,v_j
vi,vj>,表示从顶点
v
i
v_i
vi 到顶点
v
j
v_j
vj 有一条边。
- 顶点的度——无向图中,边记作 (
v
i
,
v
j
v_i,v_j
vi,vj),它等价于在有向图中存在 <
v
i
,
v
j
v_i,v_j
vi,vj> 和 <
v
j
,
v
i
v_j,v_i
vj,vi> 两条边。与顶点 v 相关的边的条数称为顶点 v 的度。
- 顶点的入度、出度——有向图中,指向顶点 v 的边的条数称为顶点 v 的入度,由顶点 v 出发的边的条数称为顶点 v 的出度。
- 有向完全图和无向完全图——若有向图中有 n 个顶点,则最多有 n(n-1) 条边,将具有 n(n-1)条边的有向图称为有向完全图,若无向图中有 n 个顶点,则最多有 n(n-1)/2 条边,将具有 n(n-1)/2 条边的无向图称为完全无向图。
- 路径和路径长度——在一个图中,路径为相邻顶点序偶所构成的序列。路径长度指路径上边的数目。
- 简单路径——序列中顶点不重复出现的路径。
- 回路——若一条路径中第一个顶点和最后一个顶点相同,则这条路径是一条回路。
- 连通、连通图和连通分量——在无向图中,如果从顶点
v
i
v_i
vi 到顶点
v
j
v_j
vj 有路径,则称
v
i
v_i
vi 和
v
j
v_j
vj 连通。如果图中任意两个顶点之间都连通,则称该图为连通图。否则,图中的极大连通子图称为连通分量。
- (无向图中)连通分量的前提:
- 是子图;
- 子图是要连通的;
- 连通子图要有极大顶点数;
- 具有极大顶点数的连通子图包含依附于这些顶点的所有边。
- 强连通图和强连通分量——在有向图中,若从
v
i
v_i
vi 到
v
j
v_j
vj 有路径,则称
v
i
v_i
vi 和
v
j
v_j
vj 连通。如果对于任意一对顶点
v
i
v_i
vi 和
v
j
v_j
vj,从
v
i
v_i
vi 到
v
j
v_j
vj 和从
v
j
v_j
vj 到
v
i
v_i
vi 都有路径,则称该图为强连通图。否则,图中的极大强连通子图称为强连通分量。
- 有根图——如果在有向图 G 里存在一个顶点 v,从顶点 v 到图 G 中其他顶点均有路径,则称 G 为有根图
- 完全图:任意两个顶点(两个不同的顶点)之间都有边的图(有向图或无向图);
- n 个顶点的无向完全图有
n
∗
(
n
−
1
)
/
2
n*(n−1)/2
n∗(n−1)/2 条边;
- n 个顶点的有向完全图有
n
∗
(
n
−
1
)
n*(n−1)
n∗(n−1) 条边;
- 权和网——图中每条边都可以附有一个对应的数,这种与边相关的数称为权,边上带有权的图称为带权图,也称为网。
- 稠密度(density)——用来表示顶点度数的平均值。
d
e
n
s
i
t
y
=
E
/
V
2
density=E/V^2
density=E/V2,
E
E
E越接近
V
2
V^2
V2,则这个图就是稠密图,反之则为稀疏图。
一、图的性质
- 对于具有n个顶点和e条边数的图,无向图有
0
≤
e
≤
n
×
(
n
−
1
)
/
2
0≤e≤n×(n−1)/2
0≤e≤n×(n−1)/2, 有向图有
0
≤
e
≤
n
×
(
n
−
1
)
0≤e≤n×(n−1)
0≤e≤n×(n−1)。
-
总度数是边的两倍,有向图的总度数是所有顶点入度和出度之和:以顶点 v 为头的弧的数目称为 v 的入度,记为
I
D
(
v
)
ID(v)
ID(v);以顶点 v 为尾的弧的数目称为 v 的出度,记为
O
D
(
v
)
OD(v)
OD(v),因此顶点v的度为
T
D
(
v
)
=
I
D
(
v
)
+
O
D
(
v
)
TD(v)=ID(v)+OD(v)
TD(v)=ID(v)+OD(v)。
- 含有V个顶点的图G是一棵树,当且仅当满足下列条件之一
- G有V-1条边,且没有环;
- G有V-1条边,且是连通的;
- 只有一条简单路径连接G的每对顶点;
- G是连通的,删除任何一条边会使他不连通。
- 只要没有回路的连通图就是树。
- 最小连通无向图(n 个顶点 ⇒ n−1 条边):无向树。当然因为连通图是彼此互通的,无向树中的任何一个顶点都可以看做树的根,因此是无向的。
- 最小有根图(n 个顶点 ⇒ n−1条边):有向树,有根图的根可以看做树根,树中因此存在树根到其他每一个顶点的路径
- 如果一个图有n个顶点和小于n-1条边,则是非连通图;如果它多于n-1条边,则必定构成一个环。连通图至少有n-1条边。包含 n 个顶点的最小连通无向图 G 恰有 n-1 条边。
- 如果一个有向图中恰有一个顶点的入度为0,其余顶点的入度均为1,则是一棵有向树。
- 一个有向图的生成森林由若干棵有向树组成,含有图中全部顶点,但只有足以构成若干棵不相交的有向树的弧。
二、图的存储结构
1. 邻接矩阵
对于如下无向图 G1:
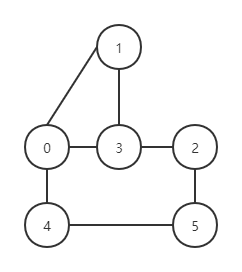
有向图 G2:
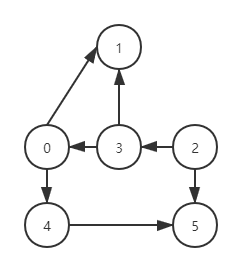
邻接矩阵是图的顺序存储结构,核心思想是:用二维数组存储图,数组的下标对应顶点,数组的值代表是否有边,例如数组中元素 v[i][j],代表顶点 i 和顶点 j,若v[i][j] 值为 1,则代表顶点 i 和顶点 j 有边。
对于无向图 G1,其邻接矩阵为
| v[0][0] (0) |
v[0][1] (1) |
v[0][2] (0) |
v[0][3] (1) |
v[0][4] (1) |
v[0][5] (0) |
| v[1][0] (1) |
v[1][1] (0) |
v[1][2] (0) |
v[1][3] (1) |
v[1][4] (0) |
v[1][5] (0) |
| v[2][0] (0) |
v[2][1] (0) |
v[2][2] (0) |
v[2][3] (1) |
v[2][4] (0) |
v[2][5] (1) |
| v[3][0] (1) |
v[3][1] (1) |
v[3][2] (1) |
v[3][3] (0) |
v[3][4] (1) |
v[3][5] (0) |
| v[4][0] (1) |
v[4][1] (0) |
v[4][2] (0) |
v[4][3] (1) |
v[4][4] (0) |
v[4][5] (1) |
| v[5][0] (0) |
v[5][1] (0) |
v[5][2] (1) |
v[5][3] (0) |
v[5][4] (1) |
v[5][5] (0) |
把二维数组的值单独列一个表
| 0 |
1 |
0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
1 |
| 1 |
1 |
1 |
0 |
1 |
0 |
| 1 |
0 |
0 |
1 |
0 |
1 |
| 0 |
0 |
1 |
0 |
1 |
0 |
可以发现,无向图的邻接矩阵的值关于主对角线对称。
对于有向图 G2,其邻接矩阵为
| v[0][0] (0) |
v[0][1] (1) |
v[0][2] (0) |
v[0][3] (0) |
v[0][4] (1) |
v[0][5] (0) |
| v[1][0] (0) |
v[1][1] (0) |
v[1][2] (0) |
v[1][3] (0) |
v[1][4] (0) |
v[1][5] (0) |
| v[2][0] (0) |
v[2][1] (0) |
v[2][2] (0) |
v[2][3] (1) |
v[2][4] (0) |
v[2][5] (1) |
| v[3][0] (1) |
v[3][1] (1) |
v[3][2] (0) |
v[3][3] (0) |
v[3][4] (1) |
v[3][5] (0) |
| v[4][0] (0) |
v[4][1] (0) |
v[4][2] (0) |
v[4][3] (0) |
v[4][4] (0) |
v[4][5] (1) |
| v[5][0] (0) |
v[5][1] (0) |
v[5][2] (0) |
v[5][3] (0) |
v[5][4] (1) |
v[5][5] (0) |
把二维数组的值单独列一个表
| 0 |
1 |
0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
0 |
0 |
0 |
| 0 |
0 |
0 |
1 |
0 |
1 |
| 1 |
1 |
0 |
0 |
1 |
0 |
| 0 |
0 |
0 |
0 |
0 |
1 |
| 0 |
0 |
0 |
0 |
0 |
0 |
- 如果是一个带权图,可以将对应的二维数组的值换成权值,这样就可以表示带权图了。
- 对于无权图的邻接矩阵表示法,存着这样一条性质
A
n
A^n
An的元素
A
n
[
i
]
[
j
]
A^n[i][j]
An[i][j]代表由顶点 i 到 顶点 j 的长度为 n 的路径的数目。(例如:以 G1 为例,
A
2
[
0
]
[
1
]
A^2[0][1]
A2[0][1]就是顶点 0 到 顶点 1 的长度为 2 的路径的数目,矩阵中第一个元素为
a
11
a_{11}
a11,第 0 行乘第1列,
A
2
[
0
]
[
1
]
=
a
11
∗
a
12
+
a
12
∗
a
22
+
a
13
∗
a
32
+
a
14
∗
a
42
+
a
15
∗
a
52
=
0
∗
1
+
1
∗
0
+
0
∗
0
+
0
∗
1
+
1
∗
0
+
0
∗
0
=
0
A^2[0][1] = a_{11}*a_{12} + a_{12}*a_{22} + a_{13}*a_{32}+ a_{14}*a_{42} + a_{15}*a_{52}= 0*1 + 1*0+0*0+0*1+1*0+0*0 = 0
A2[0][1]=a11∗a12+a12∗a22+a13∗a32+a14∗a42+a15∗a52=0∗1+1∗0+0∗0+0∗1+1∗0+0∗0=0,很明显从顶点 0 到 顶点 1 不存在长度为 2 的路径)
存储结构:
typedef struct Vertex VertexType;
struct Vertex{
int no; //顶点信息,也可能为 char类型
};
typedef struct Graph MGraph;
struct Graph{
int edges[MaxSize][MaxSize]; //邻接矩阵
int n,e; //存储顶点,边的个数
VertexType vex[MaxSize]; //存储顶点信息
};
2. 邻接表
对于如下无向图G1:
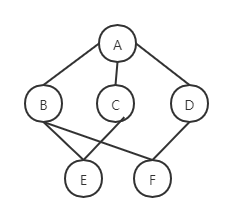
有向图 G2:
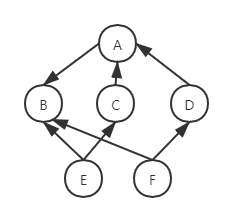
先使用数组将顶点信息存储起来:
| v[0] |
A |
| v[1] |
B |
| v[2] |
C |
| v[3] |
D |
| v[4] |
E |
| v[5] |
F |
对于无向图 G1,引入它连接的其他顶点,用数组下标表示:
| v[0] |
A |
1(B) |
2(C) |
3(D) |
| v[1] |
B |
0(A) |
4(E) |
5(F) |
| v[2] |
C |
0(A) |
4(E) |
|
| v[3] |
D |
0(A) |
5(F) |
|
| v[4] |
E |
1(B) |
2(C) |
|
| v[5] |
F |
1(B) |
3(D) |
|
很明显,对于无向图而言,其邻接表的表示方法并不唯一,但是它的邻接矩阵表示方法一定是唯一的。
对于有向图 G2,引入它出度的顶点,用数组下标表示:
| v[0] |
A |
1(B) |
|
|
| v[1] |
B |
|
|
|
| v[2] |
C |
0(A) |
|
|
| v[3] |
D |
0(A) |
|
|
| v[4] |
E |
1(B) |
2(C) |
|
| v[5] |
F |
1(B) |
3(D) |
|
存储结构:
typedef struct Vertex VertexType;
struct Vertex{
int no; //顶点信息,也可能为 char类型
};
typedef struct arcNode* ArcNode;
struct arcNode {
int adjvex; //指向哪个顶点,顶点的下标
ArcNode next; //指向下一个顶点的指针
};
typedef struct Node VNode;
struct Node{
VertexType data; //顶点信息,顶点的数据域
ArcNode first; //第一条边
};
typedef struct graph ALGraph;
struct graph{
VNode vertices[MaxSize]; //存储图
int vexnum,arcnum; //存储顶点和边的个数
};
3. 十字链表(存储有向图)
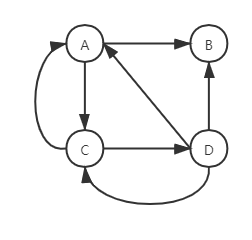
顶点结点存储顶点信息:

data为数据域,指针域 firstin:存储第一个以顶点(V[i])为弧头的边结点地址,指针域 firstout:存储第一个顶点(V[i])为弧尾的边结点地址。
表结点存储边信息:
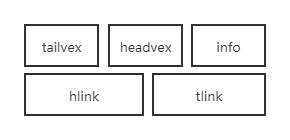
头域headvex和尾域tailvex存储的是该边(弧)的弧头和弧尾的信息,链域hlink存储的是和该边弧头一样的下一条弧,链域tlink存储的是和该边弧尾一样的下一条弧,信息域info中可以存储边的信息如权值。

观察图中顶点A,其firstin连接的是以A为弧头的第一条弧,即CA弧,其firstout连接的是以A为弧尾的第一条弧,即AB弧,而AB弧的tlink连接的是弧尾相同的下一条弧,即A为弧尾的另一条弧,AC弧,同理AB弧的hlink连接的是以A为弧头的下一条弧,即DA弧。
4. 邻接多重表(存储无向图)
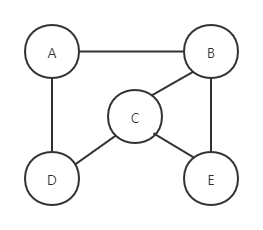
邻接多重表的思想和十字链表的思想差不多,只需要把存储顶点信息的结点稍作修改即可。

如图,顶点A的firstedge连接与该顶点相连的第一条边,即AB边,AB边的ilink连接依附于顶点A的下一条边,即AD边,jlink连接依附于顶点B的下一条边,即CB边。
三、图的遍历
在遍历过程中,需要判断图的某一顶点是否连接其他顶点,由于使用不同存储结构,其实现方式有所不同,这里均用函数名指代,不进行具体编写。
1. 图的广度优先遍历(BFS)
跟树的广度优先很相似,需要通过队列辅助实现
bool visited[MAX_Vertex_NUM]; //用于检测顶点是否都被访问过了,初始都为 false
void VisitCheck(){ //用于非连通图的情况,因为非连通图一次bfs并不能遍历完所有顶点
for(int v = 0;v < MAX_Vertex_NUM;v++)
if(!visited[v])
bfs(G,v);
}
void bfs(Grapgh G,int v){
visited[v] = true;
printf("%d",visit(v)); //visit()函数返回顶点信息
Queue q;
q.push(v);
while(empty(q) != true){
q.pop(); //队头出队
for(w = FirstNeighbor(G,v) ;w >= 0;w = NextNeighbor(G,v)){ //找出其连接的所有顶点
//FirstNeighbor()返回其连接的第一个顶点,NextNeighbor(),返回后面连接的其他顶点
//如果存在返回顶点号,不存在返回-1
if(!visited[w]){
visited[w] = true;
printf("%d",visit(w)); //visit()函数返回顶点信息
q.push(w); //w入队
}
}
}
}
2. 图的深度优先遍历(DFS)
bool visited[MAX_Vertex_NUM]; //用于检测顶点是否都被访问过了,初始都为 false
void VisitCheck(){ //用于非连通图的情况,因为非连通图一次bfs并不能遍历完所有顶点
for(int v = 0;v < MAX_Vertex_NUM;v++)
if(!visited[v])
dfs(G,v);
}
void dfs(Graph G,int v){
printf("%d",visit(v));
visited[v] = true;
for(int w = FirstNeighbor(v);w >= 0;w = NextNeighbor(v)){ //找到所有连接的顶点,每个都进行dfs
if(!visited[w])
dfs(G,w);
}
}