参考资料:
https://blog.csdn.net/qq_34213260/article/details/109133847
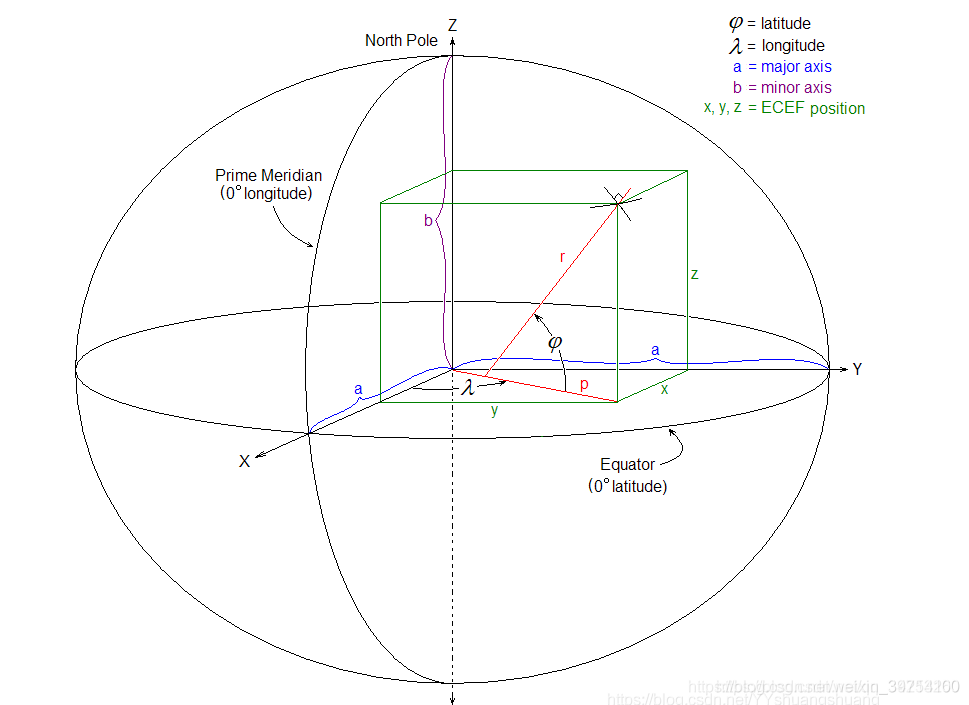
ECEF坐标系和ENU坐标系之间的关系如上图所示,各坐标系的定义在此不再赘述。
LLA坐标:Lat、Lon、Alt坐标,表示在ECEF坐标系下,其中Lat和Lon用角度(
。
^。
。)或弧度(rad)表示,Alt用米(m)表示;
ENU坐标:东北天坐标系下的坐标,该坐标系的原点需要指定,原点向东为x轴,原点向北为y轴,原点指向天为z轴,构成右手直角坐标系,该系下的坐标表示都是米制单位;
LLA坐标转换成ENU坐标的过程主要分为两步:LLA->ECEF->ENU
其中主要参数的定义如下:
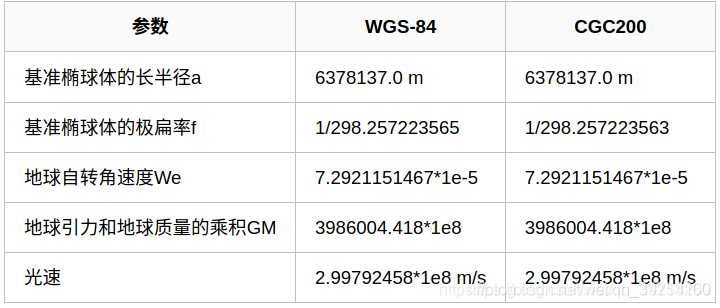
b
=
6356752.3142
b=6356752.3142
b=6356752.3142
e
2
=
f
(
2
−
f
)
e^2=f(2-f)
e2=f(2−f)
N
=
a
1
−
e
2
s
i
n
2
(
l
a
t
)
N=\frac{a}{\sqrt{1-e^2sin^2(lat)}}
N=1−e2sin2(lat)
a
其中b为椭球短半径,e为椭球偏心率
(1)LLA->ECEF:(无需给定起点,一对一转换)
从最上面一幅图中可以轻易得到同一点在这两个坐标系之间的转换关系,如下:
X
e
c
e
f
=
(
N
+
a
l
t
)
c
o
s
(
l
a
t
)
c
o
s
(
l
o
n
)
X_{ecef}=(N+alt)cos(lat)cos(lon)
Xecef=(N+alt)cos(lat)cos(lon)
Y
e
c
e
f
=
(
N
+
a
l
t
)
c
o
s
(
l
a
t
)
s
i
n
(
l
o
n
)
Y_{ecef}=(N+alt)cos(lat)sin(lon)
Yecef=(N+alt)cos(lat)sin(lon)
Z
e
c
e
f
=
(
N
(
1
−
e
2
)
+
a
l
t
)
s
i
n
(
l
a
t
)
Z_{ecef}=(N(1-e^2)+alt)sin(lat)
Zecef=(N(1−e2)+alt)sin(lat)
(2)ECEF->ENU:(需要给定起点)
假设ENU坐标系的坐标原点对应的ECEF坐标和LLA坐标分别为:
O
e
c
e
f
=
(
X
0
,
Y
0
,
Z
0
)
O_{ecef}=(X_0,Y_0,Z_0)
Oecef=(X0,Y0,Z0)
O
l
l
a
=
(
l
a
t
0
,
l
o
n
0
,
a
l
t
0
)
O_{lla}=(lat_0,lon_0,alt_0)
Olla=(lat0,lon0,alt0)
假设空间中有另一点P,且:
P
e
c
e
f
=
(
X
,
Y
,
Z
)
P_{ecef}=(X,Y,Z)
Pecef=(X,Y,Z)
则P在ENU系下的坐标为:
P
e
n
u
=
R
E
C
E
F
E
N
U
(
P
e
c
e
f
−
O
e
c
e
f
)
(1)
P_{enu}=R_{ECEF}^{ENU}(P_{ecef}-O_{ecef})\tag{1}
Penu=RECEFENU(Pecef−Oecef)(1)
其中只有
R
E
C
E
F
E
N
U
R_{ECEF}^{ENU}
RECEFENU是未知的,下面对其进行推导:
R E C E F E N U R_{ECEF}^{ENU} RECEFENU可以分解为如下三个旋转过程:ECEF–>绕 Z e c e f Z_{ecef} Zecef轴逆时针旋转 λ \lambda λ(经度)–>绕 Y e c e f ′ Y_{ecef}^{'} Yecef′轴逆时针旋转( 90 − ϕ 90-\phi 90−ϕ)( ϕ : \phi: ϕ:纬度)–>绕 Z e c e f ′ ′ Z_{ecef}^{''} Zecef′′逆时针旋转90–>ENU
上述问题是典型的空间中点不动,坐标系转动的问题,按顺序记三次旋转分别为
R
1
、
R
2
、
R
3
R_1、R_2、R_3
R1、R2、R3,则:
R
1
=
[
c
o
s
(
λ
)
s
i
n
(
λ
)
0
−
s
i
n
(
λ
)
c
o
s
(
λ
)
0
0
0
1
]
R_1= \begin{bmatrix} cos(\lambda) & sin(\lambda) & 0 \\ -sin(\lambda) & cos(\lambda) & 0 \\ 0 & 0 & 1 \end{bmatrix}
R1=⎣⎡cos(λ)−sin(λ)0sin(λ)cos(λ)0001⎦⎤
R
2
=
[
s
i
n
(
ϕ
)
0
−
c
o
s
(
ϕ
)
0
1
0
c
o
s
(
ϕ
)
0
s
i
n
(
ϕ
)
]
R_2= \begin{bmatrix} sin(\phi) & 0 & -cos(\phi) \\ 0 & 1 & 0 \\ cos(\phi) & 0 & sin(\phi) \end{bmatrix}
R2=⎣⎡sin(ϕ)0cos(ϕ)010−cos(ϕ)0sin(ϕ)⎦⎤
R
3
=
[
0
1
0
−
1
0
0
0
0
1
]
R_3= \begin{bmatrix} 0 & 1 & 0 \\ -1 & 0 & 0 \\ 0 & 0 & 1 \end{bmatrix}
R3=⎣⎡0−10100001⎦⎤
则:
R
E
C
E
F
E
N
U
=
R
3
∗
R
2
∗
R
1
=
[
−
s
i
n
(
λ
)
c
o
s
(
λ
)
0
−
s
i
n
(
ϕ
)
c
o
s
(
λ
)
−
s
i
n
(
ϕ
)
s
i
n
(
λ
)
c
o
s
(
ϕ
)
c
o
s
(
ϕ
)
c
o
s
(
λ
)
c
o
s
(
ϕ
)
s
i
n
(
λ
)
s
i
n
(
ϕ
)
]
R_{ECEF}^{ENU}=R_3*R_2*R_1= \begin{bmatrix} -sin(\lambda) & cos(\lambda) & 0 \\ -sin(\phi)cos(\lambda) & -sin(\phi)sin(\lambda) & cos(\phi) \\ cos(\phi)cos(\lambda) & cos(\phi)sin(\lambda) & sin(\phi) \end{bmatrix}
RECEFENU=R3∗R2∗R1=⎣⎡−sin(λ)−sin(ϕ)cos(λ)cos(ϕ)cos(λ)cos(λ)−sin(ϕ)sin(λ)cos(ϕ)sin(λ)0cos(ϕ)sin(ϕ)⎦⎤
将上式带入到公式(1)中可以得到:
P
e
n
u
=
R
E
C
E
F
E
N
U
(
P
e
c
e
f
−
O
e
c
e
f
)
=
[
−
s
i
n
(
l
o
n
0
)
c
o
s
(
l
o
n
0
)
0
−
s
i
n
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
−
s
i
n
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
c
o
s
(
l
a
t
0
)
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
s
i
n
(
l
a
t
0
)
]
∗
[
X
−
X
0
Y
−
Y
0
Z
−
Z
0
]
(2)
P_{enu}=R_{ECEF}^{ENU}(P_{ecef}-O_{ecef})= \begin{bmatrix} -sin(lon_0) & cos(lon_0) & 0 \\ -sin(lat_0)cos(lon_0) & -sin(lat_0)sin(lon_0) & cos(lat_0) \\ cos(lat_0)cos(lon_0) & cos(lat_0)sin(lon_0) & sin(lat_0) \end{bmatrix}* \begin{bmatrix} X-X_0 \\ Y-Y_0 \\ Z-Z_0 \end{bmatrix}\tag{2}
Penu=RECEFENU(Pecef−Oecef)=⎣⎡−sin(lon0)−sin(lat0)cos(lon0)cos(lat0)cos(lon0)cos(lon0)−sin(lat0)sin(lon0)cos(lat0)sin(lon0)0cos(lat0)sin(lat0)⎦⎤∗⎣⎡X−X0Y−Y0Z−Z0⎦⎤(2)
至此完成了LLA坐标到ENU坐标的转换,且无近似,下面对公式(2)进行近似推导
由于
X
=
(
N
+
a
l
t
)
c
o
s
(
l
a
t
)
c
o
s
(
l
o
n
)
X=(N+alt)cos(lat)cos(lon)
X=(N+alt)cos(lat)cos(lon)
Y
=
(
N
+
a
l
t
)
c
o
s
(
l
a
t
)
s
i
n
(
l
o
n
)
Y=(N+alt)cos(lat)sin(lon)
Y=(N+alt)cos(lat)sin(lon)
Z
=
(
N
(
1
−
e
2
)
+
a
l
t
)
s
i
n
(
l
a
t
)
Z=(N(1-e^2)+alt)sin(lat)
Z=(N(1−e2)+alt)sin(lat)
X
0
=
(
N
0
+
a
l
t
0
)
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
X_0=(N_0+alt_0)cos(lat_0)cos(lon_0)
X0=(N0+alt0)cos(lat0)cos(lon0)
Y
0
=
(
N
0
+
a
l
t
0
)
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
Y_0=(N_0+alt_0)cos(lat_0)sin(lon_0)
Y0=(N0+alt0)cos(lat0)sin(lon0)
Z
0
=
(
N
0
(
1
−
e
2
)
+
a
l
t
0
)
s
i
n
(
l
a
t
0
)
Z_0=(N_0(1-e^2)+alt_0)sin(lat_0)
Z0=(N0(1−e2)+alt0)sin(lat0)
所以
X
−
X
0
=
(
N
+
a
l
t
)
c
o
s
(
l
a
t
)
c
o
s
(
l
o
n
)
−
(
N
0
+
a
l
t
0
)
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
=
(
N
+
a
l
t
)
c
o
s
(
l
a
t
)
c
o
s
(
l
o
n
)
−
(
N
+
a
l
t
0
)
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
=
(
N
+
a
l
t
0
+
δ
a
l
t
)
c
o
s
(
l
a
t
0
+
δ
l
a
t
)
c
o
s
(
l
o
n
0
+
δ
l
o
n
)
−
(
N
+
a
l
t
0
)
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
=
(
N
+
a
l
t
0
)
c
o
s
(
l
a
t
0
+
δ
l
a
t
)
c
o
s
(
l
o
n
0
+
δ
l
o
n
)
−
(
N
+
a
l
t
0
)
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
+
δ
a
l
t
c
o
s
(
l
a
t
0
+
δ
l
a
t
)
c
o
s
(
l
o
n
0
+
δ
l
o
n
)
=
(
N
+
a
l
t
0
)
[
c
o
s
(
l
a
t
0
+
δ
l
a
t
)
c
o
s
(
l
o
n
0
+
δ
l
o
n
)
−
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
]
+
δ
a
l
t
c
o
s
(
l
a
t
0
+
δ
l
a
t
)
c
o
s
(
l
o
n
0
+
δ
l
o
n
)
=
(
N
+
a
l
t
0
)
[
(
c
o
s
(
l
a
t
0
)
c
o
s
(
δ
l
a
t
)
−
s
i
n
(
l
a
t
0
)
s
i
n
(
δ
l
a
t
)
)
(
c
o
s
(
l
o
n
0
)
c
o
s
(
δ
l
o
n
)
−
s
i
n
(
l
o
n
0
)
s
i
n
(
δ
l
o
n
)
)
−
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
]
+
δ
a
l
t
c
o
s
(
l
a
t
0
+
δ
l
a
t
)
c
o
s
(
l
o
n
0
+
δ
l
o
n
)
=
(
N
+
a
l
t
0
)
(
−
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
c
o
s
(
δ
l
a
t
)
s
i
n
(
δ
l
o
n
)
−
s
i
n
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
s
i
n
(
δ
l
a
t
)
c
o
s
(
δ
l
o
n
)
)
+
δ
a
l
t
c
o
s
(
l
a
t
0
+
δ
l
a
t
)
c
o
s
(
l
o
n
0
+
δ
l
o
n
)
=
(
N
+
a
l
t
0
)
(
−
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
∗
δ
l
o
n
−
s
i
n
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
∗
δ
l
a
t
)
+
δ
a
l
t
c
o
s
(
l
a
t
0
+
δ
l
a
t
)
c
o
s
(
l
o
n
0
+
δ
l
o
n
)
=
(
N
+
a
l
t
0
)
(
−
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
∗
δ
l
o
n
−
s
i
n
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
∗
δ
l
a
t
)
+
δ
a
l
t
[
(
c
o
s
(
l
a
t
0
)
−
s
i
n
(
l
a
t
0
)
∗
δ
l
a
t
)
(
c
o
s
(
l
o
n
0
)
−
s
i
n
(
l
o
n
0
)
∗
δ
l
o
n
)
]
=
(
N
+
a
l
t
0
)
(
−
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
∗
δ
l
o
n
−
s
i
n
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
∗
δ
l
a
t
)
+
δ
a
l
t
[
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
−
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
∗
δ
l
o
n
−
c
o
s
(
l
o
n
0
)
s
i
n
(
l
a
t
0
)
∗
δ
l
a
t
]
=
(
N
+
a
l
t
0
)
(
−
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
∗
δ
l
o
n
−
s
i
n
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
∗
δ
l
a
t
)
+
δ
a
l
t
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
\begin{aligned} X-X_0 &= (N+alt)cos(lat)cos(lon)-(N_0+alt_0)cos(lat_0)cos(lon_0)\\ &= (N+alt)cos(lat)cos(lon)-(N+alt_0)cos(lat_0)cos(lon_0)\\ &= (N+alt_0+\delta{alt})cos(lat_0+\delta{lat})cos(lon_0+\delta{lon})-(N+alt_0)cos(lat_0)cos(lon_0)\\ &= (N+alt_0)cos(lat_0+\delta{lat})cos(lon_0+\delta{lon})-(N+alt_0)cos(lat_0)cos(lon_0)+\delta{alt}cos(lat_0+\delta{lat})cos(lon_0+\delta{lon})\\ &= (N+alt_0)\left[cos(lat_0+\delta{lat})cos(lon_0+\delta{lon})-cos(lat_0)cos(lon_0) \right]+\delta{alt}cos(lat_0+\delta{lat})cos(lon_0+\delta{lon})\\ &= (N+alt_0)\left[(cos(lat_0)cos(\delta{lat})-sin(lat_0)sin(\delta{lat}))(cos(lon_0)cos(\delta{lon})-sin(lon_0)sin(\delta{lon}))-cos(lat_0)cos(lon_0) \right]+\delta{alt}cos(lat_0+\delta{lat})cos(lon_0+\delta{lon})\\ &= (N+alt_0)(-cos(lat_0)sin(lon_0)cos(\delta{lat})sin(\delta{lon})-sin(lat_0)cos(lon_0)sin(\delta{lat})cos(\delta{lon}))+\delta{alt}cos(lat_0+\delta{lat})cos(lon_0+\delta{lon})\\ &= (N+alt_0)(-cos(lat_0)sin(lon_0)*\delta{lon}-sin(lat_0)cos(lon_0)*\delta{lat})+\delta{alt}cos(lat_0+\delta{lat})cos(lon_0+\delta{lon})\\ &= (N+alt_0)(-cos(lat_0)sin(lon_0)*\delta{lon}-sin(lat_0)cos(lon_0)*\delta{lat})+\delta{alt}\left[(cos(lat_0)-sin(lat_0)*\delta{lat})(cos(lon_0)-sin(lon_0)*\delta{lon})\right]\\ &= (N+alt_0)(-cos(lat_0)sin(lon_0)*\delta{lon}-sin(lat_0)cos(lon_0)*\delta{lat})+\delta{alt}\left[cos(lat_0)cos(lon_0)-cos(lat_0)sin(lon_0)*\delta{lon}-cos(lon_0)sin(lat_0)*\delta{lat} \right]\\ &= (N+alt_0)(-cos(lat_0)sin(lon_0)*\delta{lon}-sin(lat_0)cos(lon_0)*\delta{lat})+\delta{alt}cos(lat_0)cos(lon_0) \end{aligned}
X−X0=(N+alt)cos(lat)cos(lon)−(N0+alt0)cos(lat0)cos(lon0)=(N+alt)cos(lat)cos(lon)−(N+alt0)cos(lat0)cos(lon0)=(N+alt0+δalt)cos(lat0+δlat)cos(lon0+δlon)−(N+alt0)cos(lat0)cos(lon0)=(N+alt0)cos(lat0+δlat)cos(lon0+δlon)−(N+alt0)cos(lat0)cos(lon0)+δaltcos(lat0+δlat)cos(lon0+δlon)=(N+alt0)[cos(lat0+δlat)cos(lon0+δlon)−cos(lat0)cos(lon0)]+δaltcos(lat0+δlat)cos(lon0+δlon)=(N+alt0)[(cos(lat0)cos(δlat)−sin(lat0)sin(δlat))(cos(lon0)cos(δlon)−sin(lon0)sin(δlon))−cos(lat0)cos(lon0)]+δaltcos(lat0+δlat)cos(lon0+δlon)=(N+alt0)(−cos(lat0)sin(lon0)cos(δlat)sin(δlon)−sin(lat0)cos(lon0)sin(δlat)cos(δlon))+δaltcos(lat0+δlat)cos(lon0+δlon)=(N+alt0)(−cos(lat0)sin(lon0)∗δlon−sin(lat0)cos(lon0)∗δlat)+δaltcos(lat0+δlat)cos(lon0+δlon)=(N+alt0)(−cos(lat0)sin(lon0)∗δlon−sin(lat0)cos(lon0)∗δlat)+δalt[(cos(lat0)−sin(lat0)∗δlat)(cos(lon0)−sin(lon0)∗δlon)]=(N+alt0)(−cos(lat0)sin(lon0)∗δlon−sin(lat0)cos(lon0)∗δlat)+δalt[cos(lat0)cos(lon0)−cos(lat0)sin(lon0)∗δlon−cos(lon0)sin(lat0)∗δlat]=(N+alt0)(−cos(lat0)sin(lon0)∗δlon−sin(lat0)cos(lon0)∗δlat)+δaltcos(lat0)cos(lon0)
同理,有
Y
−
Y
0
=
(
N
+
a
l
t
0
)
(
δ
l
o
n
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
−
δ
l
a
t
s
i
n
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
)
+
δ
a
l
t
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
Y-Y_0=(N+alt_0)(\delta{lon}cos(lat_0)cos(lon_0)-\delta{lat}sin(lat_0)sin(lon_0))+\delta{alt}cos(lat_0)sin(lon_0)
Y−Y0=(N+alt0)(δloncos(lat0)cos(lon0)−δlatsin(lat0)sin(lon0))+δaltcos(lat0)sin(lon0)
将以上两式带入到(2)中可以得到点P在ENU系下的东向坐标:
e
=
−
s
i
n
(
l
o
n
0
)
∗
(
X
−
X
0
)
+
c
o
s
(
l
o
n
0
)
∗
(
Y
−
Y
0
)
=
−
s
i
n
(
l
o
n
0
)
(
(
N
+
a
l
t
0
)
(
−
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
∗
δ
l
o
n
−
s
i
n
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
∗
δ
l
a
t
)
+
δ
a
l
t
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
)
+
c
o
s
(
l
o
n
0
)
(
(
N
+
a
l
t
0
)
(
δ
l
o
n
c
o
s
(
l
a
t
0
)
c
o
s
(
l
o
n
0
)
−
δ
l
a
t
s
i
n
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
)
+
δ
a
l
t
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
)
=
(
N
+
a
l
t
0
)
(
s
i
n
(
l
o
n
0
)
c
o
s
(
l
a
t
0
)
s
i
n
(
l
o
n
0
)
∗
δ
l
o
n
)
+
(
N
+
a
l
t
0
)
(
c
o
s
(
l
a
t
0
)
c
o
s
2
(
l
o
n
0
)
∗
δ
l
o
n
)
=
(
N
+
a
l
t
0
)
∗
δ
l
o
n
c
o
s
(
l
a
t
0
)
(
s
i
n
2
(
l
o
n
0
)
+
c
o
s
2
(
l
o
n
0
)
)
=
(
N
+
a
l
t
0
)
∗
δ
l
o
n
c
o
s
(
l
a
t
0
)
≈
a
∗
δ
l
o
n
c
o
s
(
l
a
t
0
)
\begin{aligned} e &= -sin(lon_0)*(X-X_0)+cos(lon_0)*(Y-Y_0)\\ &= -sin(lon_0)((N+alt_0)(-cos(lat_0)sin(lon_0)*\delta{lon}-sin(lat_0)cos(lon_0)*\delta{lat})+\delta{alt}cos(lat_0)cos(lon_0))+cos(lon_0)((N+alt_0)(\delta{lon}cos(lat_0)cos(lon_0)-\delta{lat}sin(lat_0)sin(lon_0))+\delta{alt}cos(lat_0)sin(lon_0))\\ &= (N+alt_0)(sin(lon_0)cos(lat_0)sin(lon_0)*\delta{lon})+(N+alt_0)(cos(lat_0)cos^2(lon_0)*\delta{lon})\\ &= (N+alt_0)*\delta{lon}cos(lat_0)(sin^2(lon_0)+cos^2(lon_0))\\ &= (N+alt_0)*\delta{lon}cos(lat_0)\\ &\approx a*\delta{lon}cos(lat_0) \end{aligned}
e=−sin(lon0)∗(X−X0)+cos(lon0)∗(Y−Y0)=−sin(lon0)((N+alt0)(−cos(lat0)sin(lon0)∗δlon−sin(lat0)cos(lon0)∗δlat)+δaltcos(lat0)cos(lon0))+cos(lon0)((N+alt0)(δloncos(lat0)cos(lon0)−δlatsin(lat0)sin(lon0))+δaltcos(lat0)sin(lon0))=(N+alt0)(sin(lon0)cos(lat0)sin(lon0)∗δlon)+(N+alt0)(cos(lat0)cos2(lon0)∗δlon)=(N+alt0)∗δloncos(lat0)(sin2(lon0)+cos2(lon0))=(N+alt0)∗δloncos(lat0)≈a∗δloncos(lat0)
类似的,可以得到n、u坐标,最终得到如下的近似结果:
P
e
n
u
=
[
e
n
u
]
=
[
a
∗
δ
l
o
n
c
o
s
(
l
a
t
0
)
a
∗
δ
l
a
t
δ
a
l
t
]
P_{enu}= \begin{bmatrix} e\\n\\u \end{bmatrix}= \begin{bmatrix} a*\delta{lon}cos(lat_0)\\a*\delta{lat}\\\delta{alt} \end{bmatrix}
Penu=⎣⎡enu⎦⎤=⎣⎡a∗δloncos(lat0)a∗δlatδalt⎦⎤
